OVERVIEW Serial composition, a development of the twentieth century, evolved from the use of ideas about the mathematics of sets in musical construction.
Diatonic Sets A set is a collection of like objects, a class of elements. The set can be made up of pitches as easily as any other kind of object. A scale can be seen as a collection of pitch objects that form a pitch set. A key signature (or consistent use of certain accidentals) defines what notes are members of a collection of pitches. This collection can be divided into smaller segments (subsets).
Any segment of a larger collection can be treated as an independent collection of pitches or as a fragment of a larger set. Notes within one of these subsets can be presented in a particular order, given a rhythm, then transposed to another level within the parent set. In other words, a motive can be created from a small group of pitches then transposed to other levels within the key.
A trichord consists of three different pitches. Like other collections of three objects, the notes of a trichord can be presented in six different orders; 123, 231, 312, 321, 213, and 132. The notes E-F-G form a diatonic set because this pattern can be found in a diatonic scale. Because of this, it can also be regarded as a subset of a diatonic scale. In the next example, each permutation was created by shifting the notes to the left. The fourth pattern was created by switching the order of E and F.
Example 1: Permutations of the subset EFG
![]()
The interval content of EFG is m2, M2, and m3 does not change no matter how the notes in the pattern are arranged. The same pattern of intervals is present in the notes BCD, the one transposition of EFG possible in the diatonic set of no accidentals.
Example 2: intervals in EFG and BCD

These two patterns and all of their permutations share common traits that distinguish them from other patterns. Thus, both are like objects that belong to the same collection, a set of sets. This set of sets includes all trichords that contain the intervals m2, M2, and m3. Membership in this set can be restricted to the natural pitches (white-keys) or be expanded to include all eleven transpositions of the set.
The pattern EFG also resides in the key of one flat, BCD in the key of one sharp. Because they can appear in more than one pitch set, these two patterns form an intersection between two diatonic pitch sets.
Example 3: Set intersection
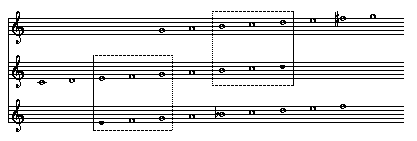
The pitches of a trichord need not be adjacent notes of a scale. Major, minor and diminished triads, for example, are diatonic subsets that contain no steps. The next example contains a diatonic subset that includes both a step and a skip. The first measure can be found in keys from zero to three flats. CDF forms unions (intersects) with four different diatonic scales. This pattern occurs at three other locations in the set of white keys, DEG, GAC, and ABD. Since all of these sets share the same interval content, they and all their permutations are members of a collection of like objects, a set of sets.
Example 4: set membership by interval content

Combinations of Notes in Ordered Subsets The number of possible combinations of notes depends on the number of notes in the pattern. For example, the notes of a particular trichord can be combined 6 ways, expressed mathematically as 3! (three factorial). The arithmetic of three factorial is 1 X 2 X 3. A tetrachord can be presented 24 unique ways (expressed 4!). Four factorial (4!) is 1 X 2 X 3 X 4. Members of a pentachord can be combined 120 ways (expressed 5!). Five factorial (5!) is 1 X 2 X 3 X 4 X 5. The interval content of a particular pattern remains unchanged regardless of how its notes are ordered.
The Diatonic Scale as a Set Key signatures define transpositions of diatonic collections. The traditional modes under one key signature are permutations of a single set of pitches.
The Diatonic Set as a Collection of Intervals Intervals in a diatonic set can be inventoried as illustrated in example 5. The inventory accounts for every interval possible between every pitch in the set. Each interval column includes an interval and its inversion. The octave and unison were not tallied because the notes in these intervals are pitches of the same name.
Example 5: Interval Inventory (interval vector) in a Diatonic Set
| A | B | C | D | E | F | G | m2 /M7 | M2 /m7 | m3 /M6 | M3 /m6 | P4 /P5 | tt |
| M2 | m3 | P4 | P5 | m6 | m7 | 2 | 1 | 1 | 2 | |||
| B | C | D | E | F | G | |||||||
| m2 | m3 | P4 | o5 | m6 | 1 | 1 | 1 | 1 | 1 | |||
| C | D | E | F | G | ||||||||
| M2 | M3 | P4 | P5 | 1 | 1 | 2 | ||||||
| D | E | F | G | |||||||||
| M2 | m3 | P4 | 1 | 1 | 1 | |||||||
| E | F | G | ||||||||||
| m2 | m3 | 1 | 1 | |||||||||
| F | G | |||||||||||
| M2 | 1 | |||||||||||
| total | 2 | 5 | 4 | 3 | 6 | 1 |
The inventory of all the intervals possible among the white keys remains unchanged regardless of the order of the notes. The same pattern of intervals can be found in any collection of pitches defined by any diatonic key signature. Thus, all diatonic modes in all keys belong to a collection of like objects, a set of diatonic sets.
Go to Set Theory, Part 2