
| pointilism | Klangfarbenmelodie |
| aggregate | complement |
| self-complementing hexachord | hexachordal combinatorial |
| prime combinatorial | inversion combinatorial |
| retrograde-inversion combinatorial | retrograde combinatorial |
| tropes | all-combinatorial |
| total serialism | multi-serial |
2. Self-help problems
Table of All-Combinatorial Hexachords
|
|
|
|
0 1 2 3 4 5 0 2 3 4 5 7 0 2 4 5 7 9 |
First three hexachords are P, I, R, RI combinatorial at one transposition level. |
| 0 1 2 6 7 8 | P, I, R, and RI at two transposition levels |
| 0 1 4 5 8 9 | P, I, R, and RI at three transposition levels |
| 0 2 4 6 8 10 | P, I, R, and RI at six transposition levels (whole tone hexachord) |
2. Assess the hexachord relationships in these rows. Under "comments" note if the second hexachord is a transformed version of the first hexachord and which all-combinatorial hexachords are used (if any). Write the normal form of the row in the second staff. Write integers inside the parentheses to indicate the prime form of each hexachords.
A. Webern: Cantata No. 1, Op. 29 Comments:

(__ __ __ __ __ __) (__ __ __ __ __ __)
B. Stockhausen: Klavierstück I Comments:

(__ __ __ __ __ __) (__ __ __ __ __ __)
C. Schuller, Fantasy for Violoncello solo, Op. 19 Comments:

(__ __ __ __ __ __) (__ __ __ __ __ __)
Solutions:
|
A. Webern: Cantata No. 1, Op. 29
|
Comments: Second hexachord is RI7 of first hexachord. Hexachords are same class but not on the list of all-combinatorial hexachords. |
|
B. Stockhausen: Klavierstück I
|
Comments: The second hexachord is not a variant of the first hexachord. Both hexachords of same class, number 1 in table of all-combinatorial hexachords. |
|
C. Schuller, Fantasy for Violoncello solo, Op. 19
|
Comments: Beginning on odd numbered notes, the row is a sequence of four M3 (IC4) and two m2 (IC1), all transposed by the same interval. No relationship between the two hexachords. But, the odd (or even) notes can be moved to the second half of the row, producing hexachords of the same type and pattern. |
Listening and Score Reading
Babbitt, Milton: All Set; Three Compositions for Piano
Berg, Alban: Lyric Suite; "Schlafend trägt man mich;" Violin Concerto (1935)
Berio, Luciano: Nones
Boulez, Pierre: Le Soleil des Eaux; Le Marteau sans maitre; Structures (1955)
Dallapiccola, Luigi: Il Prigioniero; Canti di liberazioni; Quaderno musicale di Annalibera, 1952
Krenek, Ernst: Eleven Transparencies; Sestina
Rochberg, George: Symphony No. 2 (1958)
Schoenberg, Arnold: (pre-serial) Transfigured Night; Five Orchestral Pieces, Op. 16; Six Little Piano Pieces,
Op. 19; (serial) Suite for Piano, Op. 25; Piano Piece, Op. 33a: Quartet no. 4, Op. 37; Ode to Napoleon Buonoparte, Op. 41; Piano concerto, Op.42; String Trio, Op. 45.
Schuller, Gunther: Music for Brass Quintet; Fantasy for Violoncello solo, Op. 19 (1960)
Spies, Claudio: Times Two
Stockhausen, Karlheinz: Klavierstück I; Studie Nr. II
Stravinsky, Igor: Octet for Winds; Cantata; Canticum Sacrum: In memorium Dylan Thomas.
Webern, Anton: (pre-serial) Four Songs, Op. 2; Movements for String Quartet, Op. 5; Six Pieces for Orchestra, Op. 6; Bagatelles for String Quartet, Op. 9; (serial) Symphony, Op. 21; Quartet, Op. 22; Concerto for Nine Instruments, Op. 24; Variations for Piano, Op. 27 (1936); String Quartet, Op. 28; Cantata No. 1,
Op. 29; Cantata No. 2, Op. 31 (post. 1951)
Analysis Applications
Suggested Analysis Method
When analyzing or writing a composition, construct and refer to a twelve by twelve array. During analysis or composition, label the forms in the music. Write order numbers and/or pitch class numbers by the heads of notes.
Mod 12 math is very useful in the analysis and writing of twelve-tone music. For example, The pitch class numbers of an inversion can be determined by subtracting the pitch class number of the original from 12 to produce the results below. The sum of the pitch class numbers of a row and its inversion always equals 12, assuming each form starts on the same pitch class.
| PØ | D |
C |
A |
B |
F |
E |
E | C |
A |
G |
F |
B |
| 0 | 11 | 7 | 8 | 3 | 1 | 2 | 10 | 6 | 5 | 4 | 9 | |
| IØ | D |
E |
G |
F |
B |
C |
C | E |
G |
A |
B |
F |
| 0 | 1 | 5 | 4 | 9 | 11 | 10 | 2 | 6 | 7 | 8 | 3 |
Make a twelve-by-twelve matrix of the row used in each of the following compositions. Use each matrix as a look-up table when analyzing each composition. Although rows, row forms, and combinatorial method are the primary focus of your investigation, remain aware of other factors that contribute to the musicality of the excerpts. These are factors of timbre, contour, rhythm, phrasing, texture, articulation and so on to which you would respond expressively as a performer or listener. Note how these factors relate to the twelve-tone methods employed in each composition.
Analysis 1 "Linee", N. 4 of Quaderno Musicale di Annalibera; Luigi Dallapiccola
This is the fourth in a group of eleven compositions for piano based on single row. The collection was written and named for the composer's daughter and is somewhat reminiscent of the little clavier book compiled by J. S. Bach for his wife, Anna Magdalena. The all-interval PØ version of the row in given in example 9 of this chapter.
Find and label the row forms used in this composition. Write the order numbers near the heads of the notes. In addition, write a paragraph or so describing motives, phrasing, rhythm, and texture as these patterns might influence your interpretation of the work.




© 1953 Edizioni Suvini Zerboni, Milan
Analysis 2 Semi-Simple Variations for Piano, Milton Babbitt (score following commentary).
This composition is arranged in four voices, each of which forms a row in the first twelve measures of the composition (Theme and Variation I). The top voice is PØ. Several relationships exist among the four voices. The voices form tetrachord subsets. All four notes of each subset accumulate before the next subset begins. A twelve-tone aggregate is formed by each group of three tetrachord subsets, enclosed in the vertical rectangles outlined in grey.
Also each pair of voices contains combinatorial hexachords so each pair of voices forms a twelve-tone aggregate every six dyads, enclosed in horizantal rectangles. In effect, the composition produces aggregates in two diminensions.
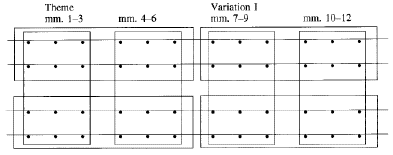
Exercise 1 The first six tetrachords are written in the bass clef under the piano part. Write the remaining six tetrachords in the same fashion under the third and fourth lines of the music. Next, write these tetrachords in prime form to determine if there is any recurrence of class of tetrachord from aggregate to aggregate.
Exercise 2 Complete a twelve-tone matrix based on PØ and determine what forms of the row were used in lines 2, 3, and 4.
Exercise 3 Write each hexachord of PØ in prime form. Look them up in the table combinatorial hexachords provided at the beginning of this application section. Using pitch class names and numbers, make a chart that shows how the hexachords form combinatorial pairs. Relate the pitches to the illustration above these exercises.
Semi-Simple Variations for piano, Milton Babbitt (1956)




©Theodore Presser Company
Analysis 3 Variations for Piano, second movement, Anton Webern, Op. 27 (Universal Edition, 1936, Theodore Presser, agent for the U. S. A.). This work and other twelve-tone compositions are included in several current anthologies.
The first eleven measures of this composition form a canon in which each voice is based on a different form of the same row. The rhythmic offset of the canon is an eight note (the second voice follows the first an eighth note later). Each voice of the canon remains in its own stave in spite of frequent clef changes. Grace notes are not incidental pitches but are members of a row. Trace the following rows in the canon. Pø is in the top stave and I2 in the bottom.
| PØ |
G |
A | F | G | E |
F |
C |
C |
D |
B |
B |
D |
| 0 | 1 | 9 | 11 | 8 | 10 | 4 | 5 | 6 | 23 | 3 | 7 | |
| I2 |
B |
A |
C |
B | D | C |
F |
F | E |
G |
G |
D |
| 2 | 1 | 5 | 3 | 6 | 4 | 10 | 9 | 8 | 0 | 11 | 7 |
Composition Applications
Write a composition based on one of the all-combinatorial hexachords. Incorporate combinatorial features. Begin by completing a twelve- by-twelve matrix to use as a reference while you work on the composition. This matrix will be a handy reference table and a good window on some of the potential of your set. Use an example from the chapter or any twelve tone composition as a model for texture and procedure. Be prepared to explain how you developed and structured your composition. Work toward a union of structure and musicality.
While this approach is quite methodical, it does not imply a mechanical or artless outcome. As you develop your composition, you will probably make artistic decisions about a number of matters not controlled by the twelve-tone method. Some of these decisions might include texture pattern, rhythm and pacing, thematic flow, contour, use of contrast, use of dissonance, and so on. Note these artistic decisions and include an account of them in any presentation you make of your composition.
Try conventional texture patterns and textural relationships when composing. Using jazz rhythm figures and accompaniment styles could generate an interesting twelve-tone composition. A song for voice and instrument(s) using established melody-with-accompaniment patterns could be effective.
1. Create the following twelve-tone rows: (1) all-interval set; (2) symmetrical set; (3) derived set [hint; use one of the six all-combinatorial hexachords, especially (0 2 3 4 5 7) and (0 1 4 5 8 9).
2. Make a twelve-by-twelve matrix for one or more of the above rows, certainly any row you plan to use in a composition. Make copies of this empty twelve-by-twelve grid as needed.
3. Write a passage of accompanied melody based on one of the rows created in the first exercise. State the row in the melody. Accompany every three PCs of the melody by the remaining nine notes in the twelve-tone aggregate (see example 17, String Quartet No. 4, Schoenberg). Experiment with accompaniment pattern possibilities (see Appendix F, Guide to the Analysis of Musical Texture). Experiment with style (i.e. jazz, lyric, popular, consonant, dissonant, and so on)
4. Write a two-voice canon based on one of the rows created in the first exercise.
5. Write a polyphonic texture that emphasizes the trichord organization of a derived set (see example 20, Concerto for Nine Instruments, Op. 30, Webern).
6. Other options (be prepared to explain how you used techniques of serial composition):
a. Write a short song for solo voice and instrumental accompaniment. Start by selecting a short poem or quote. Create your own text if you prefer.
b. Write a short composition for a solo instrument without accompaniment.
c. Write a short composition for an instrumental ensemble.
d. Write a short composition for percussion instruments based on twelve rhythm classes and/or twelve timbre classes instead of twelve pitch classes.
e. Write a short two-part composition for clapping hands based on twelve note-rest classes.
f. Write a serial round for six pop bottles each tuned to a different sound by the amount of water contained in each. Do not use tempered intonation.
g. Write a short composition for voices based on twelve mouth-sound classes (i.e. clicks, pops, glottal sounds, and so on).
h. Write a passage in which PØ is accompanied by itself in three trope versions.
Back to Twelve Tone Composition, Part 1