• time
• cost
• convenience/accessibility

In other words, we "trade off" the above "practicality" factors vs. the "certainty" that we would have by "taking a census" (also known as "canvassing") the entire population. (Although there are situations where such a census is not as costly or time-consuming, and so we might choose to go ahead and do it).

Open the link below to read a scenario that illustrates why we use sampling.

A Mayoral Fantasy

We're also currently learning in Intro to Statistics that we can get pretty close to "virtual certainty" (e.g., "95% confidence") with a 'well-chosen' (e.g., representative) sample from that population! So we may not have too much to lose, and everything to gain, by taking a sample in most cases instead of a census of the entire population!

Let's just review the process of defining a population, drawing or selecting a sample, and then "cycling back" to project or generalize the findings back to the target population!

Select sample from population and conduct study with sample subjects

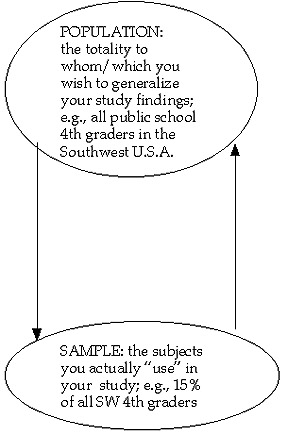Generalized or "project back" the findings/results from your sample subjects back to the population

***: how "certain" can you be that the findings from the sample will hold true for the entire population? Especially if we didnt "study" (e.g., survey or interview) everyone?

***: how "typical" or representative is the sample of this population?

"SURE THINK SOLUTION:" Study the ENTIRE POPULATION! This is called a "census" (or "canvassing" the population)

BARRIERS: Time & cost! (Is it really feasible to study everyone?)

YOU MAY NOT HAVE TO! It's been shown that the main factor in generalizability is not HOW MANY SAMPLE SUBJECTS, but rather, THE PROCESS BY WHICH THEY WERE SELECTED

***If randomly -- you're hoping you'll get a "good enough mix" on other contaminating variables or threats to validity so that they will cancel out (e.g., mix of ethnicities, I.Q.'s. & so forth). It's been shown that under random selection, a 10% sample in many cases

Let's look at the "tree" or "family" of the various sampling methods and procedures (Figure 1) and also cycle through the various types, starting below!

Before proceeding with the lesson, read this informative introduction to Sampling.

Random Sampling, non-Random Sampling and Sample Size

I. Non-Probabilistic "Family"

• Convenience
  ACCESSIBLE -- say the population is "all college sophomores currently enrolled at NAU during the Spring 1994 semester." You go to the dorms because they're "handy" & distribute your surveys to sophomore dorm residents.

  Now -- look back at the definition of "non-probabilistic" samples:
  Do you see why "not every eligible member of the population had a chance to "make it into" (be included in) your sample?

  You'll miss sophomores, single or married, living off campus!

  KEY QUESTION: REPRESENTATIVENESS. Could you have accidentally built in a bias through your convenience factor? In other words, are dorm sophomores systematically different in some way related to what you are trying to study? POTENTIAL THREAT TO VALIDITY!

• Judgment (also known as "purposive")

  MEET KEY SELECTION CRITERIA (have some sort of specialized expertise; experience; are especially articulate in the case of interview subjects)

  You can't take the chance that they'll come up in a random draw! You need them as subjects!

  They may not necessarily be a "convenience" sample (you may need to telephone an expert in New York for your interview session, for instance). BUT it is nice if you can get BOTH! accessible = convenience AND meets key selection criteria = judgment) Or, an "easy-to-get-to expert?!"

  SAME POTENTIAL THREAT TO VALIDITY == not every "expert" had a chance to "make it" into your sample! Could there have been an even "better" one out there that you just didn't know about?!

• Quota (also known as "Proportional")

  (NON-RANDOM) BALANCING -- you recognize you don't have just one overall population, but rather subgroups within that population & getting separate responses by subgroup might "make a difference" on what you're studying.

  Example: Back to "A," responses of sophomore men and women (e.g., the "gender" factor) might make a difference regarding the responses.

  In a "quota" (or "proportional") sample, you try to "match" as closely as possible the relative proportion or distribution of the subgroups in your sample.

  If there are 2 men to every woman in the sophomore population, you will select 2 men for every woman in your sample.

  QUESTION: How is this different from "stratified" (probabilistic) sampling? (Please see right-hand "family").

  ONLY ONE WAY! In stratified, you would RANDOMLY select the 2 men for every woman. In quota, you select NON-RANDOMLY (usually by convenience -- e.g., going to the dorms & handing out 2 surveys to male residents for every 1 female resident who completes the survey).

  WARNING -- gets hard to "balance" on more than 2 or 3 factors at a time ("Help; I need a 20-25 year old Hispanic female majoring in education ... !") Don't get TOO ambitious with your stratification procedures! And don't stratify if it (say, gender) isn't expected to "make a difference" on your responses!

• Snowball

  A FRIEND RECRUITS A FRIEND WHO RECRUITS A FRIEND ... Useful procedure for "rare," hard-to-find-subjects samples. For instance: "Type II diabetic women with hyperthyroidism taking a particular drug."

  You start with 1 or 2 that you can find and then ask if they can recruit another one -- who will recruit another one -- and before you know it the snowball has rolled down the hill and gotten large! And you have enough subjects for your sample!

• Are they always/necessarily "bad?" (We sometimes come out of research & statistics classes with the idea that "the only 'good' or 'best' way to sample is to draw a simple random sample!)
• Look back at the definition of "non-probabilistic" samples. Do you see how in all of the above cases, not every member of the population had some greater than zero chance of "making it" into your sample? (not accessible for convenience; not known to you for judgment; not known by your contacts for snowball, etc.)
• Thus, if the "not included" ones differed in some way from the rest that affects your study, you may have accidentally introduced a "contaminating variable" and thus a "threat to validity." With probabilistic selection, you are hoping for at least a "mix" of such contaminants, thereby reducing the threat to validity.
• BUT -- for pilot studies, instrumentation & procedure refinement, nonprobabilistic samples may be A-OK! You're using them for a "dry run," & not the real thing.
• Also, for qualitative investigations, we may need/want to pretarget subjects. In qualitative studies, you're not going for "statistical generalizability" (e.g., "with a p-value of 5%; with 95% confidence ...") but rather to reproduce and understand "real life." For instance, you may care about THIS clinic, classroom, vocational educational program & not necessarily need or want to generalize to other such classes, programs, training procedures FOR NOW.

Another resource on nonprobablistic sampling

II. Probabilistic "Family"

Read this informative introduction to Probabilistic Sampling.

Probablistic Sampling

• Simple Random Sample This is the ONLY one of the four for which every member or "element" of the population has an EQUAL chance of "making it" into your sample! For the other three, it's SOME POSITIVE (non-zero) chance but NOT NECESSARILY EQUAL.

  Steps:

  1. Identify each member (element) of the population by listing with name & number. (This is why it's so very important to describe the population precisely -- so the researcher knows "who's in & who's not") e.g.,
     • Mary Doe
     • John Smith and so forth.
  2. Make a random start (perhaps by using a table of random numbers; computer packages can also do this for you) in selecting your first sample element from the list. THE RANDOM START IS CRITICAL! This is why each element of the population has an equal chance of being chosen for your sample -- you could have "landed" on anyone's I.D. number!
  3. If you land on, say, "Number 13," then the person with Number 13 on your population list in Step One becomes your FIRST SAMPLE SUBJECT (e.g., to be interviewed, mailed a survey, and so forth).
  4. Continue randomly drawing/selecting I.D. numbers until you have as many sample subjects as you need.

• Systematic Random Sample

  Basically the same as simple random sample, EXCEPT that you MAKE THE RANDOM START and THEN SELECT EVERY "Nth" (e.g., every 3rd, 4th, 5th) NAME ON THE LIST until you have as many sample units as you need.

  This "Nth" is called your SAMPLING FRACTION (e.g., every 3rd makes the sampling fraction "1/3")

  Easier to implement, since you only need the random number table ONCE (make a random start & then put away the random number table & just pull off every 3rd person going down the list).

  CAUTION! Be aware of the fact that there could be bias in terms of your listing of population elements & how you are cycling through them with your sampling fraction. For instance, if they are arranged alphabetically, could you accidentally be "oversampling" some letters of the alphabet (R's or S's) and accidentally "undersampling" others (Z's, Q's) by "missing" them with your sampling fraction? This is called "periodicity" in the sampling frame (or listing).

  SOLUTION? Randomize ("jumble") the listing in the frame or change the sampling fraction!

• Stratified Random Sample

  Basically the same as "quota" or "proportional," except that once you subdivide your OVERALL population into SUBGROUPS or "STRATA" (singular form is "stratum"), then you draw the sample within each stratum using a probabilistic procedure. For instance (please see next page):

  
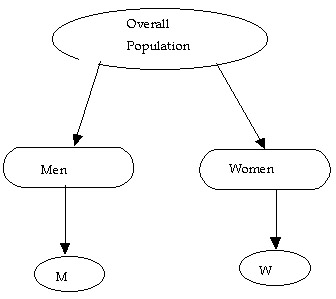
  1. We first stratify the population (in this case, by gender); and then;
  2. We proceed to draw "sub-samples" (e.g., using a simple random, systematic, or some other probabilistic sampling procedure) from each "stratum."

     Do you see how this is different from a quota sample?

     In the quota sample, the draw of men & women was not at random (could be convenience or judgment, for instance) Here, if you are doing a simple random sample within each stratum, you'd need to repeat the steps under "A" twice (e.g., separate lists or sampling frames for men and women).

     Two ways to plan strategy in selecting how to "balance" the strata:"

     1. If there are "close to" an EQUAL number of subjects within each stratum, draw an equal number for your sample too.

     2. If the ratios of subjects within each stratum are vastly UNEQUAL (e.g., 7 men to 3 women), try to maintain that same ratio in your sample selection. This is known as "p.p.s." (probability proportional to size) stratified random sampling.

• Cluster Sampling

  Instead of drawing individuals as your sampling elements, you recognize that "they come in groups" (clusters). So -- you randomly draw the clusters instead!

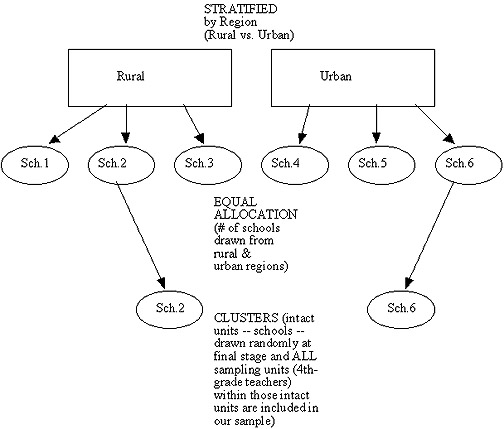
PLEASE NOTE: The researcher has RANDOMLY DRAWN 2 CLUSTERS (intact schools 1 & 6) from the 6 total schools; AND THEN, HE/SHE PROCEEDS TO "USE" (e.g., test, survey, interview)EVERY SAMPLING UNIT (child) IN THOSE RANDOMLY DRAWN SCHOOLS.

ADVANTAGE (of cluster over simple random sampling): Might save time & money drawing whole groups & taking everyone in them (e.g., saving trips to sites).

"TRICK QUESTION!" For a "good" cluster sample, do we want the sampling units (e.g., kids within the selected classrooms) to be VERY SIMILAR OR VERY DIFFERENT?

Remember the goal of randomization is to get a "good enough mix" on other potential confounding variables or threats to validity!

Got it? Yes -- VERY DIFFERENT (so as to get that "good mix on all other stuff" (that could have "caused" or "confounded" what we are actually trying to study -- the treatment, for instance).

Also, look at it this way : if the kids within each classroom were virtually identical, particularly on those other variables (e.g., ethnicity, gender, I.Q.) why would it even be necessary to study ALL of them (within that cluster)?! In the limit, if they WERE identical, YOU'D ONLY NEED ONE!!!

See the "savings" (over simple random) a bit better now?

If we can get such a "good mix" by saving ourselves a step & drawing intact clusters vs. individuals, it might be more cost- efficient that way!

Remember -- to get to your "ultimate" or "primary sampling unit" (e.g., kids) you may need to "pass through" a number of "intermediate sampling units"

• Kids come "nested" in classrooms ...
• which are "nested" in schools ...
• which are "nested" in districts ...
• which are "nested" in states ... etc., etc.

A "multistage" sample recognizes that you may choose different sampling procedures at different stages! For instance:

1. Select states via simple random sample;
2. Then stratify districts in chosen states by rural vs. urban for a stratified random sample;
3. Then select every 5th school (systematic) within the lists of districts chosen in Step Two;
4. Then draw intact classrooms randomly from the schools chosen in Step Three (cluster sample);
5. And finally, test (sample) every child in those randomly drawn classrooms (still part of cluster).

You research superstars are first-rate! The StatCat salutes ya'!!!

Go on to Assignment5-1-1
or
Go back to Population and Sampling

E-mail M. Dereshiwsky at statcatmd@aol.com
Call M. Dereshiwsky at (520) 523-1892

Copyright 1998 Northern Arizona University
ALL RIGHTS RESERVED