Lesson3-1-1



	EDR610 : The Class : Variables/Hypotheses : Variables : Lesson3-1-1

Understanding Variables

So far, research superstars, we've discussed how the research question (or problem statement) "drives" all other parts of the research plan (Figure 1 in your first module).

Last time (Module # 2), we also learned that these research questions/problem statements can be sorted or grouped into "families." These families depend on:

what you are trying to answer or find out;

certain "keywords" in the problem statement or research question (e.g., "what is/what are," or identifying would imply a descriptive question/statement)
Next, we'll be zeroing in on these questions/statements and trying to identify the variables associated with our questions/statements.

These variables will also be closely linked to our "scales of measure" (first module in Statistics), as we'll soon see!

***Click on the "sample solution set/extra examples" . Print this out and keep it handy for reference as you work through this module and particularly for review before you do Assignment #3!

What Is a "Variable?"
Broadly speaking, a "variable" is a "target measurement" or "outcome" of your problem statement/research question. Variables are the "things" we're measuring, or collecting data (information) on, or forming groups on, in order to conduct our research study and answer our question(s).
This is why it's important to be able to identify the "key variables" within our problem statement/research question.
Hopefully, this will become a bit clearer with some examples. But first, let's take a moment to identify the distinction between a "variable" and a "constant!"

Variables vs. Constants
- A variable can also be thought of as something whose value (quantitative or qualitative) can be different for each research subject.
- A constant, on the other hand, always has the SAME value (quantitative or qualitative) for each research subject.
  As an example, let's look at the following:
  
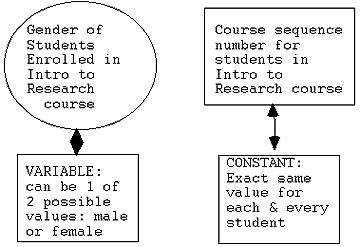
  Do you see why, in the above, "Gender" (of students enrolled in EDR 610, Intro to Research, course by modem, SS I) is a 'variable?' It can 'vary' (albeit not very much ... only two possible 'values', but still .... !) from student to student: male or female.
  P.S. Can't resist a tie-in, statistics fans! Do you also see how the variable of "gender" is nominally scaled as well?
  The numbers assigned to code in a student's gender are strictly arbitrary and just labels! These numeric codes "wouldn't mean anything as numbers!" Doesn't matter if you decide to assign:
  '1' for male and '2' for female; or
  ' 576' for male and '384' for female!
  In contrast, our particular course sequence number in EDR 610, SS I, Intro to Research is a constant! That's because it stays exactly the same for each and every student (research subject; research unit)! Again, don't ask me what it is ... I'm just making this up ... let's say "31849"!
  To sum up:
Variables Can Be Defined or Measured in More than One Way
How you choose to EXACTLY measure or define variables is something called "operationally defining your variables." This will depend on 'what it is you want to know, exactly, about this variable,' which in turn comes from how you are using it in your problem statement or research question.
We'll talk more about "operational definitions" two packets from now.
For now, though, let me give you just one example.
Suppose you have the variable of "kind of school."
Admittedly, this is broad in nature and could, conceivably, be defined or measured many ways!
For one thing, you could have:

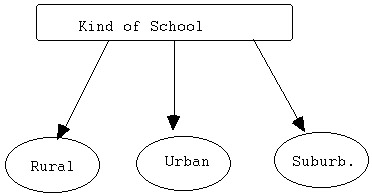
You'd want to define it this way if you think, say, that the region might 'make a difference' on something you're studying.
Or suppose, instead, that you need and want to find out about the level taught of each school, rather than the region in which it is located. (Again, this would come from your research question or problem statement.) In this case, you might have something like the following:

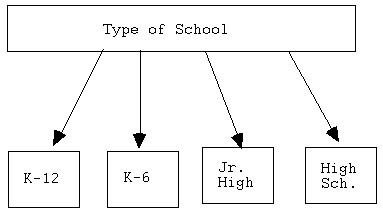
I realize that, in the above sample "mini-graphic," I didn't list all the possible choices, or categories. This was just intended to give you the general "gist" of the fact that the variable of "type of school" can be defined in a totally different way (from the first example, of 'region').
But just to digress for a moment, if you're defining a variable by breaking it down into "subgroups," such as BOTH of the above 2 alternative definitions (e.g., "grouping by region" and "grouping by level taught"), your grouping or coding categories need to possess two (2) key properties; namely, they must be:

mutually exclusive (that is, each 'unit' -- in this case, school, can go in one and only one grouping category -- not overlap into 2 or more); and

exhaustive (you must 'cover all the bases;' that is, there needs to be SOME category that EVERY 'unit' gets classified into -- even if it means ... ah, the bane of developing 'good' category codes!!! ... creating a 'catch-all' category like "Other" or "Miscellaneous" if you absolutely need to!)
Finally, back again to the issue of "defining your variables in potentially different ways," you could have instead needed or wanted to measure the variable of 'type of school' according to its 'current student population.'
One way to do this (& by the way, not a bad idea for practical reasons to start with it THIS way even if you'll opt for the 2nd possibility to be discussed shortly) is to collect the 'raw data' by 'exact student population;' e.g.:

... and so on and so forth!
On the other hand, you could have chosen to define the "student population" itself NOT in discrete or 'raw' values but by subgroups or subcategories; e.g.,:

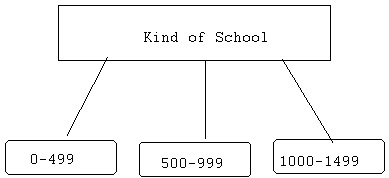
... & again, so on and so forth 'till you form all of your "mutually exclusive & exhaustive" subgroups or categories (as per the "2 key qualities" of making such groupings: please refer back to pg. 7!)
Now ... please take a moment & compare the 2 alternative forms of defining "school population" again.
Do you see why I mentioned, back on pg. 7, that it's probably a good idea to go ahead and code in the 'raw values' (exact student population for each school) EVEN IF you think you'll really need and want this information only by groups?
Suppose you START with the following ranges of grouping:
0 - 499;
500 - 999;
1,000 - 1,499 ... etc., etc.
BUT THEN LATER YOU CHANGE YOUR MIND! and you say, "That's way too broad." I need the information broken down or categorized by 'smaller ranges' than that; e.g.,:
0 - 399;
400 - 799;
800 - 1,199; .... etc., etc.
Well, if you originally had the data or values in 'raw form,' it'll be a breeze to recategorize them by computer into the new smaller ranges! On the other hand, if all you did originally was to collect the information from the sampled schools by your first code (e.g., on a survey, "Please check off the one choice that best describes your current student enrollment: (a) 0-499; (b) 500 - 999, etc.") ... then you'll be out of luck if you later change your mind and try to regroup them in a different (especially 'smaller-range') way!
OK ... I hope you've gotten the idea that many variables can be defined in more than one way, depending on what you want to know and why you want to know it!
The above examples of the different ways we 'played with' defining 'type of school' as a variable ought to lead in nicely into another 'set of labels' we can apply to many variables!

Quantifiable variables can be defined as "discrete" or "continuous."
Ah -- method to the madness of that sometimes gol-darn frustrating first Statistics packet on "Scales of Measure!"
That's because your practice in identifying and distinguishing among the 4 types (nominal, ordinal, interval ratio) and the 2 broader "families" (Nominal + Ordinal belong to "Categorical;" Interval + Ratio belong to "Continuous!") will fit perfectly here!
Let's have a look now at discrete and continuous variables.

That's right! You first go back and identify which scale of measure applies to that variable. Then you'll know whether it is "discrete" (categorical) or "continuous" (same name!)
Just to review and practice:
- When we defined 'type of school' by its 'raw value,' or 'exact current school population,' that would be ratio scaled (possible 'true zero;' school still under construction so no students go there YET!) So ... that way, the variable of 'type of school' is also a 'continuous' variable!
- On the other hand, when we subgrouped this current school population into the ordered ranges of, say, "0-499," "500-999," and so forth, do you see how that would be "ordinal" data (limited number of categories, & some order -- e.g., size -- to those categories) -- which would also make this a 'discrete' variable?
So... just to give some more examples:

Please take a moment and convince yourself (using the "discrete vs. continuous" graphic on pg. 10, and after classifying each of the above into its scale of measure) why a given variable, above, is either 'discrete' or 'continuous!' (And of course, PLEASE don't hesitate to ask your cyberspace Commander m.d. if you should have questions! We'll successfully navigate you through 'em!)
Also, one reminder about the above 2 labels: the terms "discrete" and "continous" apply ONLY to those variables that are QUANTIFIABLE. They wouldn't be pertinent to QUALITATIVE (in words) data or variables, such as "Teachers' attitudes towards unionization," IF this variable is being measured by interviewing teachers and recording their attitudes in words.
This brings us to yet another way that many variables can sometimes be labeled:

Some variables can be defined as "independent" or "dependent" in nature.

These will apply to "experimental"-type studies. We've briefly discussed some features of "experiments" in Module #2 (e.g., forming groups such as "traditional lecture" vs. "hands-on science instruction"; doling out one or more treatments depending on these groups -- that is, one group gets the 'treatment' of the hands-on science instruction while the control group gets the traditional lecture method of teaching; and trying to establish a 'tight control' over those other factors which could creep in and contaminate the results of what we WANT to assess or measure -- e.g., did the "type of instruction" affect or influence master of basic science concepts?) We will be learning more about experimental-type studies when we get into "families of research design" a bit later on in the course! For now, if the above summary gives you the 'general gist' of what an 'experiment' is about, that'll do it!
For now, IF you DO have an experimental-type research question, problem statement and associated 'experimental design,' you can also label your variables as follows:

The independent variable is the one you use to form or "make" your groups. You'd give an overall name or label to the independent variable, and each subgroup that's contained within it is called a "level" of that variable.
Let's stick with the preceding example and hopefully this will become clearer ...

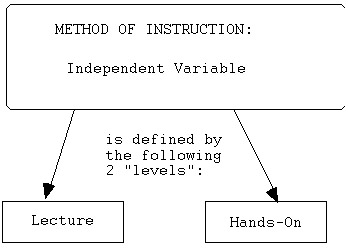
Please note, from the preceding example, that I thought up an "overall descriptive label" for the independent variable itself: "Method of Instruction." Next, I identified each of its "levels;" that is, how many subgroups are contained within it. And each level was named according to the 'distinguishing characteristics' of that subgroup (e.g., Level # 1: "Traditional Lecture Method").
*** WARNING!!! It's easy to confuse the "independent variable itself" with its "levels!!!"
In other words, it would be wrong to say, "The independent variable in the preceding example is the hands-on method of science instruction." That's only PART of it! or ONLY ONE LEVEL of the (TOTAL) independent variable, "Method of Instruction!"
If this helps, the independent variable is like identifying the whole forest, and the various trees, flora, fauna that together make up that forest would be like its levels!!!
Now for the dependent variable:

The dependent variable is the one that you expect to change, or vary, as a result of the independent variable. It might be thought of as the outcome. You'll be measuring this outcome to see what effect(s) the independent variable had on the dependent variable.
In the above experimental study example, we might envision holding constant as many other factors as we can, and then making sure to give the students in BOTH groups (traditional and hands-on instruction methods) the SAME test of science achievement.
Therefore, in this case, the dependent variable would be "science achievement." Again, it's the one we expect will 'vary,' or 'be different,' as a result of the method of science instruction.
By measuring this dependent variable (and controlling for as many other variables as possible; please see # 7, below, for a label for THOSE!), we will get an indication of the relative effect of the "method of instruction" (independent variable) upon the target outcome of "science achievement" (dependent variable).
Please remember: the terms "independent" and "dependent" variables are relevant ONLY for EXPERIMENTAL-TYPE studies.
You can also have MORE THAN ONE independent and/or dependent variable in a given study. For instance, we might have defined two dependent variables;

Students' science achievement (as above; e.g., measured by a standardized test); and

Students' self-esteem (also measured by a standardized test).

"Confounding" variables are those variables whose effects we could not control for in our experimental study, and which might have 'crept in' to contaminate or influence our outcome (dependent variable).
In other words, we think/hope that if we do see a difference in average science achievement scores -- let's say they're higher on average in the hands-on instructional group -- that it's 'because of' or 'due to' our independent variable of "method of instruction."
But suppose also that we haven't done as good and thorough a job as we might have liked in anticipating and controlling for other possible causal/contaminating factors!
Suppose, for instance, that we also happen to have twice as many boys as girls in the hands-on instructional group! And that prior research, theory, practice, etc., have consistently shown that boys will tend to do better in science than girls at that particular age regardless of methods of instruction.
Then: "Gender" has turned out to be a confounding variable. Its effects have become 'confounded with' the effect of the independent variable, "method of instruction," that we really intended or wanted to study.
Finally ... we're almost home ... one more classification scheme for 'variables!'
Research more information on confounding variables and a couple more examples.

In predictive studies (remember, 'prediction' is a special case of 'correlation' where one 'thing' precedes the other and we use information about the first to forecast or predict the second), we can apply the terms "predictor" and "criterion" to the variables.

The "predictor" is the first variable -- the one we have information about and are 'using';

The "criterion" is the second --the one being predicted.

Remember: these labels only apply to those correlational studies where there is such a time order or sequence!

If you'll remember the example of 'self-esteem' & 'academic achievement' from Module #2, where they were CIRCULAR (each fed back on and affected the other), for that example the terms would not apply (since they're kind of in an 'endless loop' rather than one strictly leading into, or being used to predict, the other).

Also, as with all of the preceding examples, you could possibly have more than one predictor and/or criterion variable! Again, it depends on your particular research question or problem statement!

- - -

WHEW!!! We've had quite a workout on variables today!

Let's see if we can summarize!

Summary Notes

A variable is something that can take on different values (quantitative or qualitative) for different subjects in a given research study. A constant, on the other hand, carries the exact-same value for all subjects in a study.
Quantitative variables are:
For experimental studies only:
Confounding variables are things/conditions/effects, and so forth that you were unable to control for. Therefore they 'crept in and contaminated' the effects of your independent variable. That is: you think it's the independent variable that "caused" or "affected" your dependent variable(s) -- but actually, it was partially or entirely the "confounder" that did so.
For predictive studies (correlational with a distinct time order or sequence to the variables): The predictor is the one that "happens first;" The criterion is the one "being predicted."

Go on to Assignment 1: Scales of Measurement
or
Go back to Understanding Variables

E-mail M. Dereshiwsky at statcatmd@aol.com
Call M. Dereshiwsky at (520) 523-1892