K-Means

Introduction

Iterative algorithms have the following pattern: each rank has a compute phase, then ranks exchange information, and this process repeats until the terminating criterion is met (all iterations have been executed, the algorithm converges, etc.). This pattern is common in many applications, such as stencil applications and k-means clustering. In this module, we will implement a distributed-memory k-means clustering algorithm.

Student Learning Outcomes

• Understand the k-means algorithm by implementing it from scratch.
• Understand common patterns in distributed-memory programs (alternating phases of computation and communication).
• Reason about performance based on algorithm complexity.
• Reason about performance based on communication patterns and volumes.
• Reason about resource allocation.
• Reason about how the algorithm could be improved beyond the scope of the assignment.

Prerequisites

Some knowledge of the MPI API and familiarity with the SLURM batch scheduler.

MPI Primitives Used

There are no required primitives. However, the following primitives may be very useful.

• MPI_Scatter
• MPI_Allreduce

Files Required

• kmeans_starter.c
• iono_57min_5.16Mpts_2D.txt

Problem Description

The naive k-means clustering algorithm assigns each point to the closest centroid by computing the Euclidean distance between each point and each of the $k$ centroids. Then, using the positions of all points assigned to each centroid, the positions of the centroids are updated to reflect the mean of the data points assigned to the centroids. These two steps, point assignment to centroids and updates to centroid positions, continue until the algorithm converges where no points change their assignment to the centroids between two iterations. However, the algorithm does not tell us how “good” the point assignments to clusters are, and selecting $k$ and the initial set of centroids is not straightforward. Like all clustering algorithms, the goodness of the clusters depends upon data characteristics and domain knowledge.

An example illustration is shown in Figure 1 with $k=3$ clusters, where 15 iterations are required until convergence. The colors denote the assignment to the centroids.

The naive k-means algorithm has the following complexity: $O(Nkdi)$, where $N$ is the number of data points to cluster, $k$ is the number of centroids, $d$ is the data dimensionality, and $i$ is the number of iterations needed until the algorithm converges. In this exercise, we will use a static number of iterations such that the algorithm does not necessarily converge. Using a deterministic number of iterations allows us to study the performance of the algorithm.

The major steps in the (sequential) algorithm are summarized below.

1. Generate initial centroid positions.
2. Assign all points in the dataset to the nearest centroid using the Euclidean distance.
3. Update the location of the centroids for the next iteration.
4. Repeat steps 2 and 3 until the convergence criterion is met.

Q1: What component of the algorithm is straightforward to parallelize?

Q2: When parallelizing the algorithm, what component of the algorithm requires communication between process ranks?

Parallelization Problems

Each process rank can compute the distance between some fraction of the $N$ points to each of the $k$ centroids in parallel. The difficulty in parallelizing the algorithm is updating the positions of the centroids, since it requires global knowledge of the assignments of each point to each centroid.

A couple of ideas that could be used to solve this problem are given below. You do not need to use either of these ideas in your solution, and you may skip reading this information and go directly to the programming assignment. You may come back to this section once you start thinking about the synchronization component of the algorithm.

Idea 1

At each communication step, perform a global operation (hint: this may include an MPI_Allgather) that communicates the assignment of each point to each centroid on each rank with all other ranks (see Figure 2). Then, have each rank independently compute the positions of the centroids. A negative consequence of this idea is that each rank will perform duplicate work by redundantly computing the positions of each centroid at each rank, and it requires sending $O(N)$ data elements to each rank.

Idea 2

Another option is to use weighted means to reduce the overhead of sending $O(N)$ elements. In this case, you can use weighted means to update the positions of the means. By sending the weighted means to each process rank, the amount of data sent to each rank is only $k+kdp$. Since typically $kdp \ll N$ this requires less data to be transferred than idea 1 above.

An example of computing weighted means using a set of integers is given below:

Consider the numbers $Q=$ {2, 4, 6, 8, 10, 12, 14} which need to be averaged between $p=2$ process ranks. Observe that the global mean of these numbers is 8.

Let’s split the set above into $R$ and $S$ where $Q=R\cup S$, and assign $R=$ {2, 4, 6 } to rank 0 and $S=${8, 10, 12, 14} to rank 1, where $|R|=3$ and $|S|=4$, and $w_0$ and $w_1$ denote the weighted means at these ranks.

• $w_0=(2+4+6)/7$ and $w_1=(8+10+12+14)/7$.
• Adding the weighted means together, we obtain: $w_0+w_1=8$, which is the global mean that we wish to compute.
• Note that to compute the global mean, the values of $|R|+|S|=7$ needs to be known.
• In the context of the k-means algorithm, since each process rank only knows the local counts of how many points are assigned to each centroid, the ranks need to exchange the sizes of their local sets of points assigned to each centroid before computing the weighted mean (i.e., $w_0+w_1$ above).
• By performing weighted sums at each rank, the communication overhead compared to the first solution significantly decreases, as the sums need to be transferred, not the entire global mean assignment array that maps each point to its closest centroid.

Programming Activity #1

Write a distributed-memory k-means algorithm using the following guidelines. You may want to program a sequential version of the k-means algorithm before attempting to write the distributed-memory version.

• Use and modify the starter file: kmeans_starter.c.
• We will use a 2-dimensional dataset, but write the program such that it could process any data dimensionality. The dataset is as follows: iono_57min_5.16Mpts_2D.txt.
• The program will take as input the following information on the command line: the number of lines in the dataset file, the dimensionality of the data, the number of centroids ($k$), and the dataset file.
• An example of running the program with $p=1$ process rank is as follows: mpirun -np 1 -hostfile myhostfile.txt ./kmeans <N> <DIM> <K> <dataset file>
• You will have rank 0 assign $\lfloor N/p \rfloor$ points to each process rank. If $N~\mathrm{mod}~p~!=0$, you must assign the “leftover” points to the other ranks. You may assign all leftover points to the last rank, since the number of leftover points will be small.
• Each rank will read the entire dataset. This may be useful depending on how you perform the communication/synchronization step when updating the positions of the centroids (ideas above).
• Initialization of means: We will simply assign the first $k$ points in the dataset to be the initial means.
• Number of iterations: Use 10 iterations. Since each iteration has the same amount of work to compute, we will not run the algorithm to convergence. Using 10 iterations is sufficient for studying the performance of the algorithm.
• Empty centroids: The naive k-means algorithm does not define what happens if a centroid is empty. That is, it’s possible that a centroid will have no members at a given iteration. Some options to remedy this are to remove the centroid, or randomly assign the centroid a new position. To deal with this corner case, we will simply reinitialize the mean to be located at position 0,0.

In your code, you will make time measurements of the following:

• The total execution time defined by the time taken by the longest executing rank.
• The maximum cumulative time spent performing distance calculations.
• The maximum cumulative time spent updating centroids, including performing synchronization between ranks.
• All of the three time components can be computed using an MPI_Reduce with a maximum operation.
• Note that since you are computing the maximum cumulative time to compute the distance calculations and updating centroids, these two times are not expected to add up to the total execution time.

When running your program on the cluster, make sure your job script(s) and program conforms to the following guidelines:

• All programs are compiled with the -O3 flag.
• Use a single node.
• Use the exclusive flag for all experiments so that your results are not polluted by other users running on the node.
• Make sure you run all of your experiments on a single node generation.
• You will time the execution of your program using MPI_Wtime(). Begin timing after you have imported the dataset and have allocated memory for the dataset (as shown in the starter file).
• Run three time trials for each execution configuration. Report the average response time in seconds (s). All other metrics you will report are derived from the response time.

In your report, include tables with the following information for executions with $p=1, 4, 8, 12, 16, 20$ process ranks, and $k=2, 25, 50, 100$. This will allow us to examine how performance varies with $p$ and $k$. You will create three tables showing the total response time, maximum cumulative time spent performing distance calculations, and maximum cumulative time spent updating means. Additionally, compute the speedup of your algorithm using the data in Table 1. Include all job scripts in the submitted archive. The job script may be the same for all executions. Example template tables are given below.

Table 1: Total response time.

# of Ranks ($p$)	$k=2$	$k=25$	$k=50$	$k=100$	Job Script Name (*.sh)
1
4
8
12
16
20

Table 2: Maximum cumulative time spent performing distance calculations.

# of Ranks ($p$)	$k=2$	$k=25$	$k=50$	$k=100$	Job Script Name (*.sh)
1
4
8
12
16
20

Table 3: Maximum cumulative time spent updating means, including performing synchronization between ranks.

# of Ranks ($p$)	$k=2$	$k=25$	$k=50$	$k=100$	Job Script Name (*.sh)
1
4
8
12
16
20

Table 4: Speedup computed using the data in Table 1.

# of Ranks ($p$)	$k=2$	$k=25$	$k=50$	$k=100$
1
4
8
12
16
20

Answer the following questions using the data collected in the tables above:

• Q3: Describe how you implemented your algorithm.

• Q4: Explain the (potential) bottlenecks in your algorithm.

• Q5: How does the algorithm scale when $k=2$? Explain.

• Q6: How does the algorithm scale when $k=100$? Explain.

Validation

Here are several things to consider when validating your algorithm:

• At each iteration, have one rank output the values of each centroid (e.g., rank 0).
• Make sure that at each iteration each rank has identical centroids.
• Changing $p$ should not change the values of the centroids.

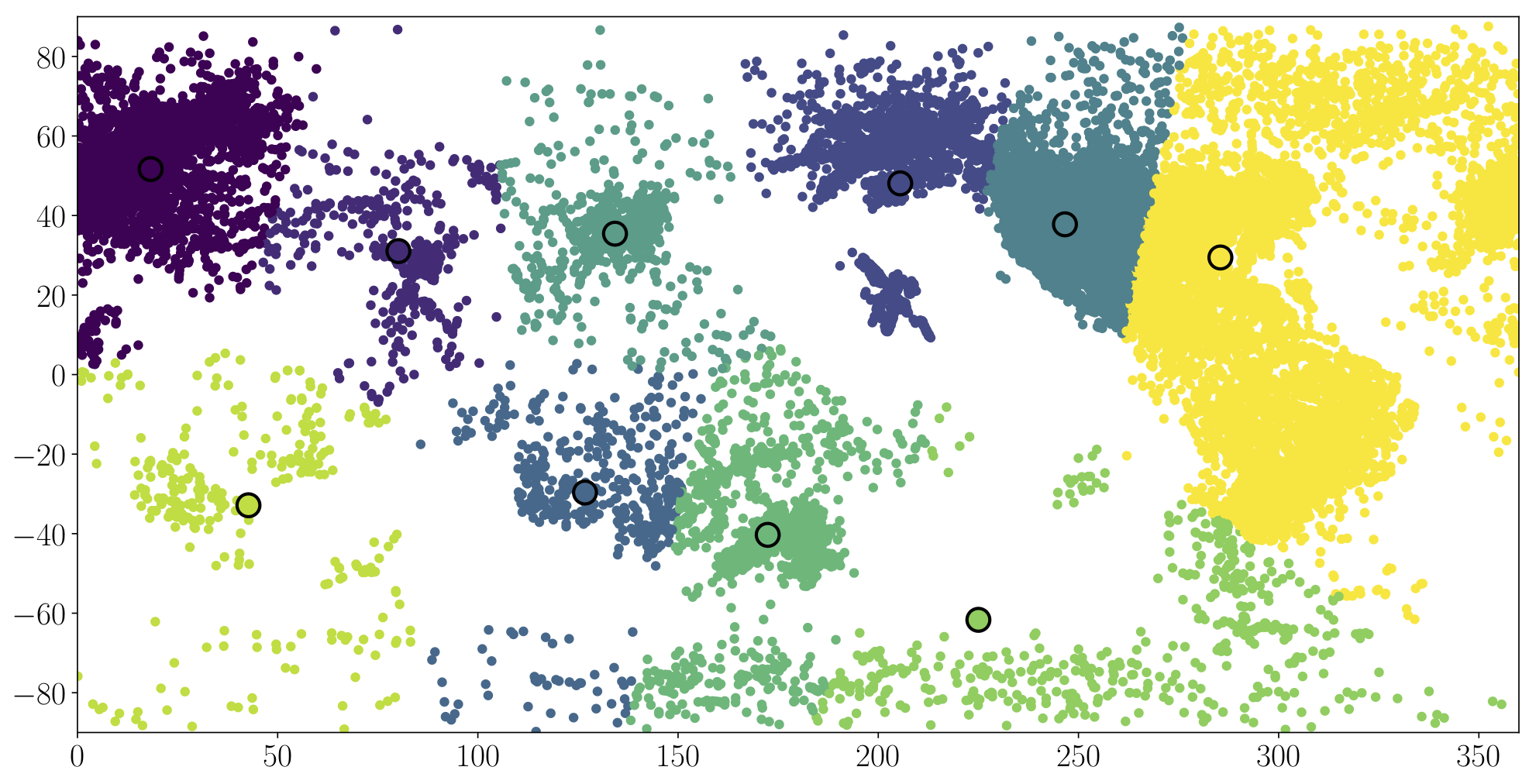
To validate that your k-means algorithm works correctly, submit plots showing the positions of the centroids at the end of the second to last iteration, which will correspond to the centroids computed to be used by the last iteration. Since the algorithm updates the centroids at iteration $l$ to be used at iteration $l+1$, the correct set of centroids used for the assignment phase in the last iteration corresponds to the centroids computed at the second to last iteration.

Submit 4 plots corresponding to $k=2, 25, 50, 100$ centroids. Ensure that the x dimension is plotted in the range [0, 360] and the y dimension between [-90, 90].

An example plot is shown in Figure 3 below that plots the positions of the centroids and the assignment of points to these centroids for $k=10$. You are not required to plot the assignment of points to centroids, but you may prefer to do this anyway to convince yourself that the algorithm works as intended.