Graph Rubbling Numbers

Rubbling moves

One of the following:

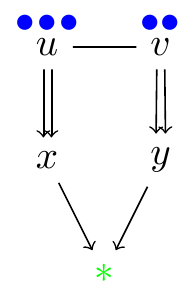
Pebbling Move (v, v → u):

One can move two pebbles from a given vertex to one of its neighbors. However, only one pebble reaches the neighbor since the other is paid as a toll along the edge.
before during after
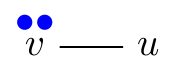
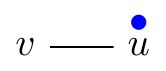
figure pebStart.png figure pebEnd.png
p(v, u) = (2, 0) p(v, v → u)(v, u) = (0, 1)
figure p1.png figure p2.png figure p3.png

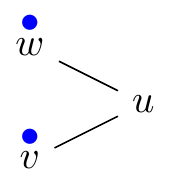
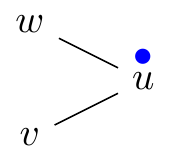
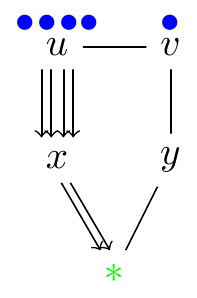
Strict rubbling move (v, w → u):

The two pebbles can come from different neighbors.
before during after
figure rubStart.png figure rubEnd.png
p(v, w, u) = (1, 1, 0) p(v, w → u)(v, w, u) = (0, 0, 1)
figure rub1.png figure rub2.png figure rub3.png

Connie & Peter

Peter the Pebbler and Connie the Configurer play the following game on a graph G. Peter buys t very expensive pebbles and gives them to Connie. Of course, Peter doesn’t want to spend too much money if he can avoid it. Connie distributes a configuration p:VG → ℕ of pebbles onto the vertices of G and chooses a root vertex r. Peter will win the game if he can place a pebble on r after a sequence of rubbling moves; otherwise, Connie wins the game.

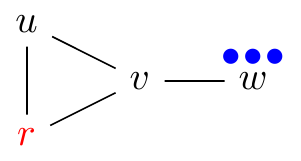
Solvability

In the case that Peter wins we say that p is r-solvable (otherwise r-unsolvable). If p is r-solvable for every r then p is called solvable.
r-solvable r-unsolvable
figure unsolvable.png figure solvable.png

Rubbling number

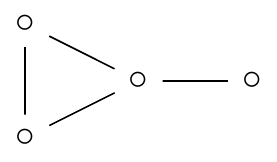
The pebbling number of G is denoted ρ(G) and equals the fewest number of pebbles Peter must buy in order to guarantee victory. That is, if Peter buys ρ(G) pebbles then every possible configuration of Connie’s is solvable, while if Peter buys ρ(G) − 1 pebbles then Connie can find a configuration that is r-unsolvable for some r.
ρ(G) = 4, π(G) = 5
figure graph.png

Bounds

d = diameter, n = number of vertices
  1. More options upper bound. ρ(G) ≤ π(G) It is easier to reach a vertex with more move options.
  2. Depth lower bound. 2d ≤ ρ(G) Connie can place all the pebbles on a vertex as distance d from r.
  3. Pigeon whole upper bound.ρ(G) ≤ (n − d + 1)(2d − 1 − 1) + 2 [3].
  4. ρ(G) < n is possible.

First Results

  1. Paths. ρ(Pn) = 2n − 1
  2. Cliques. ρ(Kn) = 2
  3. Wheels. ρ(Wn) = 4
  4. Complete bipartite graphs. ρ(Km, n) = 4
  5. Cubes. ρ(Qn) = 2n
  6. Petersen. ρ(P) = 5
  7. Lemke. ρ(L) = 8

Trees

ρ(T) = 2p1 + ∑mi = 22pi − 1 − m + 1 where (p1, …, pm) is the length sequence of a maximum path partition for T.
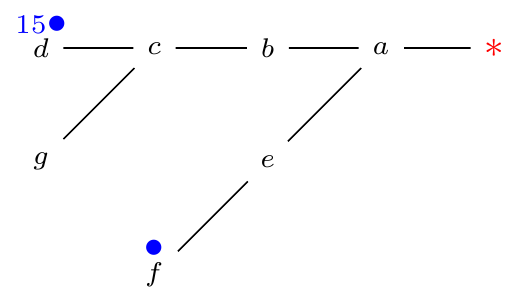
figure tree.png
ρ(T) = (24 − 1) + (21 − 1) + (20 − 1) + 1 = 17 where (4, 2, 1) is the length sequence.

Cycle graphs

ρ(C2k) = 2k and ρ(C2k + 1) = ⌊(7⋅2k − 1 − 2)/(3)⌋ + 1 where Cn is the cycle graph with n vertices. [1]
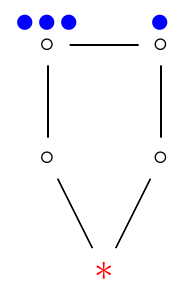
figure cycle1.png figure cycle2.png figure cycle3.png

Graham’s conjecture

The conjecture fails for rubbling.
C3□C3 C3
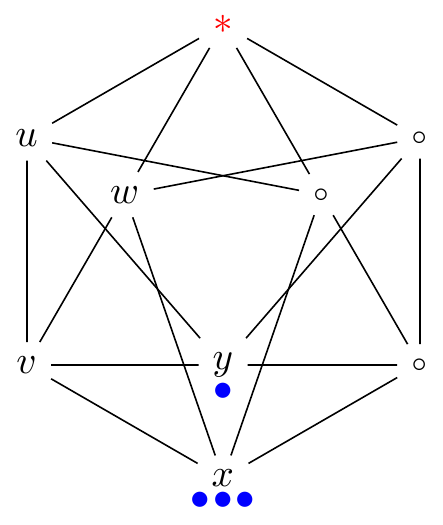
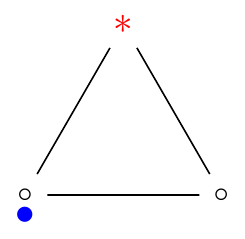
figure C3C3.png figure C3.png

Complexity

The decision problem whether a vertex is reachable from a given configuration is NP-complete.

Optimal Rubbling Numbers

Minimum number ρopt(G) of pebbles in a chosen pebble distribution from which any vertex is reachable is called the optimal rubbling number.
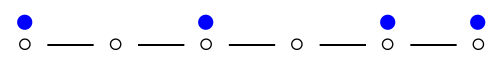
figure P6Opt.png

Results

  1. Paths. ρopt(Pn) = ⌈(n + 1)/(2)⌉
  2. Cycles. ρopt(Cn) = ⌈(n)/(2)⌉
  3. Cliques. ρopt(Kn) = 2
  4. Wheels. ρopt(Wn) = 2
  5. Complete bipartite graphs. ρopt(Km, n) = 3
  6. Petersen. ρopt(P) = 4
  7. Prisms ad Ladders. ρopt(P3k + r□P2) = 2k + 1 + ⌈(r)/(3)⌉ [5]
  8. Caterpillars. [4]

Cover Rubbling Conjecture

The cover pebbling and cover rubbling numbers are the same for all graphs. Stacking Lemma remains true.

t-Rubbling Numbers

Minimum number ρt(G) of pebbles to make any vertex reachable with t pebbles no matter how the pebbles are distributed is the t-rubbling number.

Results

  1. Trees. ρt(T) = t2p1 + ∑mi = 22pi − 1 − m + 1
  2. m-ary trees. [2]
  3. Conjecture: Cycle. ρt(C2k + 1) = (2k − 17 + ( − 1)k)/(3) + (t − 1)2k and ρt(C2k) = t2k.

References

Please let me know if any article about rubbling is missing.
  1. Christopher Belford and Nándor Sieben, Rubbling and optimal rubbling of graphs, Discrete Math. 2009, volume 309, number 10 , p. 3436-3446,
  2. Lisa Danz, Optimal t-rubbling of complete m-ary trees. 2010. REU project report, University of Minnesota Duluth, Department of Mathematics and Statistics.
  3. Gyula Y. Katona and Nándor Sieben, Bounds on the Rubbling and Optimal Rubbling Numbers of Graphs, Graphs and Combinatorics 29(3): 535-551 (2013)
  4. László Papp, Optimal rubbling numbers of graphs (in Hungarian). 2010. thesis, Budapest University of Technology and Economics, Department of Computer Science and Information Theory.
  5. László Papp, Optimal rubbling numbers of prisms and ladders (in Hungarian). 2011. preprint, Budapest University of Technology and Economics, Department of Computer Science and Information Theory.
  6. Gyula Y. Katona and László Papp, The Optimal Rubbling Number of Ladders, Prisms and Möbius-ladders, Discrete Appl. Math. 209 (2016), 227–246. http://arxiv.org/abs/1411.0923
  7. Kyle Murphy, On t-Restricted Optimal Rubbling of Graphs, M.S. Thesis, East Tennessee State University
  8. Ervin Györi, Gyula Y. Katona, and László F. Papp, Optimal pebbling and rubbling of graphs with given diameter, https://arxiv.org/abs/1708.09177
  9. Robert Beeler, Teresa Haynes, Kyle Murphy, An introduction to t-restricted optimal rubbling, Congr. Numer. 228 (2017), 129–140.
  10. Robert Beeler, Teresa Haynes, Kyle Murphy, 1-restricted optimal rubbling on graphs, Discuss. Math. Graph Theory 39 (2019), no. 2, 575–588.
  11. Robert Beeler, Teresa Haynes, Rodney Keaton, Domination cover rubbling, Discrete Appl. Math. 260 (2019), 75–85.
  12. Ervin Győri, Gyula Y. Katona, László F. Papp, Optimal pebbling and rubbling of graphs with given diameter, Discrete Appl. Math. 266 (2019), 340–345.
  13. Zheng-Jiang Xia , Zhen-Mu Hong, A note on the optimal rubbling in ladders and prisms, https://arxiv.org/abs/1909.01703

Links