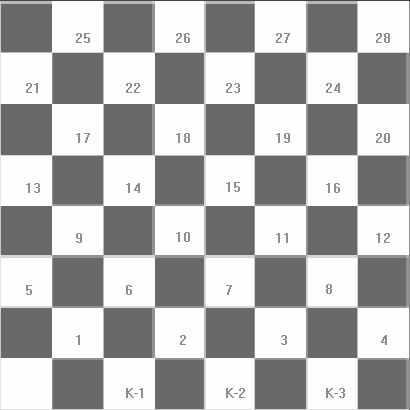
The game of jumping checkers is played on an ordinary 8x8 checkerboard
(chessboard). Three red kings are placed in the 2nd,
3rd, and 4th white squares in the bottom row of the board
(squares labeled "K-1", "K-2" and "K-3" below) and single black checkers are placed on
b of the remaining 28 white squares in all but the bottom row of the board
(labeled 1,2,...,28 below).
The only moves allowed are for red kings to "jump" black checkers diagonally,
forward or backward (this requires an "open" square immediately beyond the black
checker jumped, as in
the traditional board game). A black checker is removed from the board
once it has been jumped. The kings may continue to move as long
as jumps are available.
|
Part I
(a) How many arrangements of b black checkers are possible?
(b) Show that a black checker located in any of the following squares can
never be jumped: 4, 5, 6, 7, 8, 12, 13, 14, 15, 16, 20, 21,
22, 23, 24, 25, 26, 27, 28.
(c) Show that no more than nine jumps are possible regardless of the value of b.
(d) For a fixed b=1, 2, 3, 4, 5, 6, 7, 8, or 9,
assume that each possible configuration
of b checkers over the 28 squares is equally likely. Let
Xb denote the random variable number of jumps made. Show
that the values of Xb that have non-zero probability
are x = 0, 1, ..., b, and
find the probability distribution of Xb.
P(X9=9) is easy to calculate, but other
cases can be tedious to compute, particularly for larger values of
b.
|
(b) If a player wishes to maximize expected winnings (or minimize
expected losses), what value of b should the player choose?
