Set Theory Part 2
Terms and Problems
1. Terms:
| nondiatonic subset | octave equivalence | |
| pitch class | enharmonic equivalence | |
| pitch class numbers | interval numbers | |
| interval class | interval class numbers | |
| interval vector | dyad | |
| trichord | tetrachord | |
| octachord | undecachord | |
| quintad | tetrad | |
| hexachord | heptichord | |
| hexad | septad | |
| pentachord | normal form | |
| inversion(mod 12) | transposition(mod 12) | |
| prime form | set class | |
| mapping onto | mapping onto self | |
| unordered collection | aggregate | |
| simultaneity | ordered collection |
2. Which of the twelve trichord set classes (012 , 013, 014, 015, 016, 024, 025, 026, 027, 036, 037, and 048) cannot be found in a diatonic scale?
3. Make a trichord dictation exercise for use in class. Using the trichords in exercise 2, let 0 be any pitch except C. Let the notes be in any order except that in exercise 2. Displace the middle note up or down an octave.
4. Compose a melody based on one of the trichords in exercise 2. Use transpositions and a new order of pitches each time the trichord occurs.
5. Self-help problems and solutions
Problem 1: Identify the intervals according to the information needed to fill in the blanks in the grid. Use the first column of the grid as a sample solution.
| interval number | 4 | 7 | 2 | 9 | 5 | 11 | 8 | 1 | 3 | 10 | 6 |
| interval name | M3 | ||||||||||
| interval class | 4 |
Problem 2: Identify the intervals according to the information needed to fill in the blanks in the grid. Use the first column of the grid as a sample solution.
| interval number | 10 | 6 | 3 | 1 | 8 | 11 | 5 | 9 | 2 | 7 | 4 |
| interval name | m7 | ||||||||||
| interval class | 2 |
Problem 3: Identify the intervals according to the information needed to fill in the blanks in the grid. Use the first column of the grid as a sample solution.
| interval number | 9 | 2 | 7 | 4 | 1 | 8 | 11 | 5 | 6 | 10 | 3 |
| interval name | M6 | ||||||||||
| interval class | 3 |
Problem 4: Identify the intervals according to the information needed to fill in the blanks in the grid. Use the first column of the grid as a sample solution.
| interval number | 3 | 10 | 1 | 6 | 8 | 11 | 5 | 2 | 7 | 4 | 9 |
| interval name | m3 | ||||||||||
| interval class | 3 |
Solution 1:
| interval number | 4 | 7 | 2 | 9 | 5 | 11 | 8 | 1 | 3 | 10 | 6 |
| interval name | M3 | P5 | M2 | M6 | P4 | M7 | m6 | m2 | m3 | m7 | tt |
| interval class | 4 | 5 | 2 | 3 | 5 | 1 | 4 | 1 | 3 | 2 | 6 |
Solution 2:
| interval number | 10 | 6 | 3 | 1 | 8 | 11 | 5 | 9 | 2 | 7 | 4 |
| interval name | m7 | tt | m3 | m2 | m6 | M7 | P4 | M6 | M2 | P5 | M3 |
| interval class | 2 | 6 | 3 | 1 | 4 | 1 | 5 | 3 | 2 | 5 | 4 |
Solution 3:
| interval number | 9 | 2 | 7 | 4 | 1 | 8 | 11 | 5 | 6 | 10 | 3 |
| interval name | M6 | M2 | P5 | M3 | m2 | m6 | M7 | P4 | tt | m7 | m3 |
| interval class | 3 | 2 | 5 | 4 | 1 | 4 | 1 | 5 | 6 | 2 | 3 |
Solution 4:
| interval number | 3 | 10 | 1 | 6 | 8 | 11 | 5 | 2 | 7 | 4 | 9 |
| interval name | m3 | m7 | m2 | tt | m6 | M7 | P4 | M2 | P5 | M3 | M6 |
| interval class | m3 | 2 | 1 | 6 | 4 | 1 | 5 | 2 | 5 | 4 | 3 |
Problem 5:
1. Write the trichord, C D![]() F, in the first row of the 3 X 3 grid (a123).
F, in the first row of the 3 X 3 grid (a123).
2. Write the melodic inversion of the trichord in the first column (1abc), using "C" as a common tone.
3. Use 1b and 1c as the starting notes of transpositions of the original trichord (1abc).
4. Reading from top to bottom, what version of the original pattern is present in columns 2 and 3?
5. Reading from right to left, what version of the original pattern is present in rows a, b, and c?
6. Reading from bottom to top, what version of the original pattern is present in columns 1, 2, and 3?
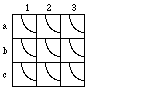
Problem 6:
1. Write the pitch class numbers 0 3 4 of the quadrants (pie wedges) of row a.
2. Write the pitch class inversion numbers in the wedges of column 1 (12 - pitch class number).
3. Write the transpositions of row a in rows b and c. Add the value in 1b to the original pitch class number. If the result is greater than 11, subtract it from 12. Repeat the operation operation by adding the value of 1c to the original pitch class number.
4. Assuming that pitch class 0 = C![]() , use the pitch class number to determine which pitch class should be written in each box.
, use the pitch class number to determine which pitch class should be written in each box.

Sample of Interval Vector Procedure
| pitch class in hexachord | Interval Classes | ||||||||||
| 0 | 1 | 3 | 4 | 5 | 8 | 1 | 2 | 3 | 4 | 5 | 6 |
| C |
D |
E |
E | F |
A |
1 | 1 | 2 | 1 | ||
|
D |
E |
E | F |
A |
1 | 1 | 1 | 1 | |||
|
E |
E | F |
A |
1 | 1 | 1 | |||||
| E | F |
A |
1 | 1 | |||||||
| F |
A |
1 | |||||||||
| total | ICs | 3 | 2 | 3 | 4 | 3 | 0 | ||||
| C | D | F |
| B | C | E |
| G | A | C |
solution 6:
| 0 C | 3 E | 4 F |
| 9 B | 0 D | 1 D |
| 8 A | 11 C | 0 D |
Problem 7: Complete an interval vector using the sample solution on the previous page as a guide. Derive the pitch names from the pitch class numbers.
| pitch class in hexachord | Interval Classes | ||||||||||
| 0 | 1 | 4 | 5 | 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 |
| F |
F |
A |
B |
D |
D | ||||||
| total | ICs | ||||||||||
Problem 8: Complete an interval vector using the sample solution as a guide. Derive pitch names from the pitch class numbers.
| pitch class in hexachord | Interval Classes | ||||||||||
| 0 | 1 | 2 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 |
| A | |||||||||||
| total | ICs | ||||||||||
Solution 7:
| pitch class in hexachord | Interval Classes | ||||||||||
| 0 | 1 | 4 | 5 | 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 |
| F |
F |
A |
B |
D |
D | 1 | 1 | 2 | 1 | ||
|
F |
A |
B |
D |
D | 1 | 2 | 1 | ||||
| A |
B |
D |
D | 1 | 1 | 1 | |||||
|
B |
D |
D | 1 | 1 | |||||||
|
D |
D | 1 | |||||||||
| total | ICs | 3 | 0 | 3 | 6 | 3 | 0 | ||||
Solution 8:
| pitch class in hexachord | Interval Classes | ||||||||||
| 0 | 1 | 2 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 |
| A |
B |
B |
E |
E | F | 1 | 1 | 1 | 1 | 1 | |
|
B |
B |
E |
E | F | 1 | 2 | 1 | ||||
| B |
E |
E | F | 1 | 1 | 1 | |||||
|
E |
E | F | 1 | 1 | |||||||
| E | F | 1 | |||||||||
| total | ICs | 4 | 2 | 0 | 2 | 4 | 3 | ||||
Problem 9: Complete an interval vector using the sample solution as a guide. Use the pitch class numbers to determine pitch names.
| pitch class in hexachord | Interval Classes | ||||||||||
| 0 | 2 | 4 | 5 | 7 | 9 | 1 | 2 | 3 | 4 | 5 | 6 |
|
B |
|||||||||||
| total | ICs | ||||||||||
Sample of Inversion Procedure
| 1 | 2 | 1 | 1 | 3 | Interval number (note to note) | |
| C |
D |
E |
E | F |
A |
note names of Pø |
| 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| 0 | 1 | 3 | 4 | 5 | 8 | original hexachord - pitch class number |
| 0 | 11 | 9 | 8 | 7 | 4 | pitch class number of I |
| C | B | A |
A |
G | E | note names of I |
| - 1 | - 2 | - 1 | - 1 | - 3 | Interval number (note to note, a double check, should be same as top line.) |
Solution 9:
| pitch class in hexachord | Interval Classes | ||||||||||
| 0 | 2 | 4 | 5 | 7 | 9 | 1 | 2 | 3 | 4 | 5 | 6 |
|
B |
C | D |
E |
F | G | 1 | 1 | 1 | 2 | ||
| C | D |
E |
F | G | 1 | 1 | 2 | ||||
| D |
E |
F | G | 1 | 1 | 1 | |||||
|
E |
F | G | 1 | 1 | |||||||
| F | G | 1 | |||||||||
| total | ICs | 1 | 4 | 3 | 2 | 5 | 0 | ||||
Problem 10: Work out an inversion of the original hexachord. Use the sample procedure on the previous page as a guide. Fill in all blanks.
| Interval number (note to note) | ||||||
| D | note names of Pø (use pitch class numbers) | |||||
| 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| 0 | 2 | 4 | 6 | 8 | 10 | original hexachord - pitch class number |
| pitch class number of I | ||||||
| note names of I | ||||||
| Interval number (note to note) (a double check, should be same as top line.) |
Problem 11: Work out an inversion of the original hexachord. Use the sample solution as a guide. Fill in all blanks.
| Interval number (note to note) | ||||||
| C | note names of Pø (use pitch class numbers) | |||||
| 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| 0 | 1 | 3 | 6 | 7 | 9 | original hexachord - pitch class number |
| pitch class number of I | ||||||
| note names of I | ||||||
| Interval number (note to note) (a double check, should be same as top line.) |
Solution 10:
| 2 | 2 | 2 | 2 | 2 | Interval number (note to note) | |
| D | E |
F |
G |
A |
C | note names of Pø (use pitch class numbers) |
| 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| 0 | 2 | 4 | 6 | 8 | 10 | original hexachord - pitch class number |
| 0 (12=0) | 10 | 8 | 6 | 4 | 2 | pitch class number of I |
| D | C |
A |
G |
F |
E | note names of I |
| -2 | -2 | -2 | -2 | -2 | Interval number (note to note) (a double check, should be same as top line.) |
Solution 11:
| 1 | 2 | 3 | 1 | 2 | Interval number (note to note) | |
| C |
D |
E |
F |
G | A | note names of Pø (use pitch class numbers) |
| 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| 0 | 1 | 3 | 6 | 7 | 9 | original hexachord - pitch class number |
| 0 (12=0) | 11 | 9 | 6 | 5 | 3 | pitch class number of I |
| C | B | A |
F |
F |
E |
note names of I |
| -1 | -2 | -3 | -1 | -2 | Interval number (note to note) (a double check, should be same as top line.) |
Sample of Transposition Procedure
| 1 | 2 | 1 | 1 | 3 | Interval number (note to note) | |
| C |
D |
E |
E | F |
A |
note names of Pø |
| 5 | 5 | 5 | 5 | 5 | 5 | T interval ( 5 ) |
| 0 | 1 | 3 | 4 | 5 | 8 | original hexachord + pitch class number |
| 5 | 6 | 8 | 9 | 10 | 1* | *(13 - 12 = 1) pitch class number of Transposition (Pn) |
| F |
F |
G |
A |
B |
D |
note names of Pn |
| 1 | 2 | 1 | 1 | 3 | Interval number (note to note) (a double check, should be same as top line.) |
Problem 12: Work out a transposition of the original hexachord. Use the sample solution as a guide. Fill in all blanks.
| Interval number (note to note) | ||||||
| G | note names of Pø (use pitch class numbers) | |||||
| 8 | 8 | 8 | 8 | 8 | 8 | T interval (8) |
| 0 | 1 | 2 | 6 | 7 | 8 | + pitch class numbers in original hexachord |
| pitch class number of Transposition (Pn) | ||||||
| note names of Pn | ||||||
| Interval number (note to note) (a double check, should be same as top line.) |
Problem 13: Work out a transposition of the original hexachord. Use the sample solution as a guide. Fill in all blanks.
| Interval number (note to note) | ||||||
|
B |
note names of Pø (use pitch class numbers) | |||||
| 6 | 6 | 6 | 6 | 6 | 6 | T interval (6) |
| 0 | 2 | 3 | 5 | 6 | 9 | + pitch class numbers in original hexachord |
| pitch class number of Transposition (Pn) | ||||||
| note names of Pn | ||||||
| Interval number (note to note) (a double check, should be same as top line.) |
Solution 12:
| 1 | 1 | 4 | 1 | 1 | Interval number (note to note) | |
| G |
A |
A |
D |
D |
E |
note names of Pø (use pitch class numbers) |
| 8 | 8 | 8 | 8 | 8 | 8 | T interval (8) |
| 0 | 1 | 2 | 6 | 7 | 8 | + pitch class numbers in original hexachord |
| 8 | 9 | 10 | 2 (14-12) | 3 | 4 | pitch class number of Transposition (Pn) |
|
E |
E | F | A |
B |
B | note names of Pn |
| 1 | 1 | 4 | 1 | 1 | Interval number (note to note) (a double check, should be same as top line.) |
Solution 13:
| 2 | 1 | 2 | 1 | 3 | Interval number (note to note) | |
|
B |
C |
C |
E |
E | G | note names of Pø (use pitch class numbers) |
| 6 | 6 | 6 | 6 | 6 | 6 | T interval (6) |
| 0 | 2 | 3 | 5 | 6 | 9 | + pitch class numbers in original hexachord |
| 6 | 8 | 9 | 11 | 0 (12-12) | 3 | pitch class number of Transposition (Pn) |
| E |
F |
G | A |
B |
C |
note names of Pn |
| 2 | 1 | 2 | 1 | 3 | Interval number (note to note) (a double check, should be same as top line.) |
Problem 14: Find and label the prime form of these tetrachords (C E F![]() G
G![]() , C D
, C D![]() E
E![]() A
A![]() , C E A B)
, C E A B)
[Hint: Prime form is the most compact version of normal form and its inversion. Normal form is the most compact version of all rotations of a pitch set. The first step in determining these forms is to arrange the PCs in low-to-high order. ] Rotate the notes of the original pattern. Let the lowest note of each rotation be PC#0. The inversion of normal form is the same as the normal form of the inversions. Arrange it in lowest-to-highest order, assigning Ø to the lowest note. As a shortcut to determining prime form, read normal form top-to-bottom, making the highest note Ø.



Solution 14:



Back to Set Theory, Part 1