Introduction

BA501 : The Class : Statistics : Regression Analysis : Introduction
Regression Introduction
Introduction

Introduction- Lesson 1

Regression analysis is used primarily for predictive purposes. The result of the least squares method of simple regression is an estimated equation based on a sample. Statistics generated from a sample (the intercept and slope of the regression equation) are used as estimates of parameters in the population. Hypotheses tests are used to draw conclusions about the a claimed values for the populations parameters. Confidence intervals are used to attempt to quantify the populations parameters within a range of possible values. Analysis of variance is used to determine the coefficient of determination as a measure of the strength of the regression equation.

1. Least Squares Line- Simple Linear Regression

(A) Least Squares ( Regression ) Line-

(1) The "best fitting" line through the bivariate data (ordered pairs, x,y).

(2) For any x there are two associated y values:

(a) the observed value for y (in the ordered pair), and

(b) the predicted value, yhat, on the regression line.

(c) d = y - yhat

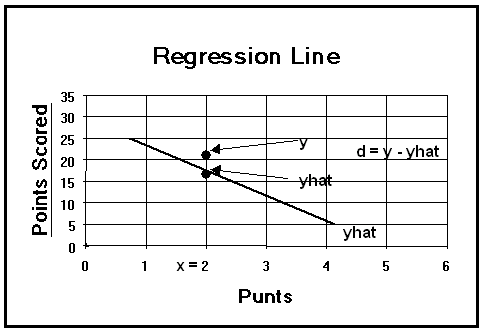
(d) S d = S (y - yhat) = 0

[1] When calculating a variance: S (x - xbar) = 0. Solved by squaring,

S (x - xbar)² (click me)

(e) d² = S (y - yhat)²

(3) "Best fitting" means that the sum of the squared deviations of the observed data (ys) from the associated predicted values (yhats) is minimized.

(a) d² = S (y - yhat)² ( minimum possible)

(b) d² = SSE (Sum of Squared Errors)

(c) d² = SS_y - [SCP_xy]² / SS_x

where,

[1] SCP_xy = [ S xy - (S x)( S y) / n]

[2] SS_x = [S x²- (S x)² / n]

[3] SS_y = [S y²- (S y)² / n]

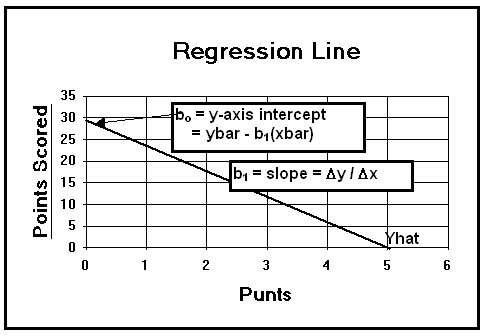
(B) Slope of the Regression Line:

(1) b₁ = D y / D x (click me)

(2) b₁ = [S xy - (S x)( S y) / n] / [S x²- (S x)² / n]

(3) b₁ = SCP_xy / SS_x

where,

(a) SCP_xy = S xy - (S x)(S y) / n

(b) SS_x = S x²- (S x)² / n

(C) b_o = y-intercept of the Regression Line:

b_o = ybar - b₁(xbar)

where

(1) xbar = S x / n

(2) ybar = S y / n

(D) Least Squared Regression Line Equation

(1) Yhat = b_o + b₁[x]

(2)

The regression line can be completely defined knowing the slope and the y axis intercept. True False (click one)

A simple linear regression is represented by a __________ line.

2. The Simple Linear Regression Model

(A) Use a statistical model to represent a "true but unknown" relationship between X and Y.

(B) Y = b _o + b ₁[X] + e

(1) b _o + b ₁are unknown parameters.

(2) e = error, the random part of model.

(3) b_o (y axis intercept, statistic based on a sample) is an estimate of b _o

(4) b₁ (slope, statistic based on a sample) is an estimate of b ₁

(C) Assumptions for the Simple Linear Regression Model-

(1) X is non-random.

(2) For each x, the random component is e (distribution of errors).

(a) The mean of each e component is zero.

(b) Each e component is normally distributed.

(c) The variance of each e component is same for each X.

(d) The errors are independent of each other. (click me)

(D) Estimating the Error Variance, s ²e

(1) s² = s ²e(hat) = estimate of s ²e = SSE / [n- 2]

= MSE (click me)

(a) MSE = Mean Square Error = SSE / (n - 2)

(2) SSE = S (y - yhat)²

= SS_y - [SCP_xy]² / SS_x

where,

[a] SS_y = S y² - (S y)² / n

[b] SCP_xy = S xy - (S x)(S y) / n

[c] SS_x = S x² - (S x)² / n

(3) s = Ö s² = Ö [s ²e(hat)] = Ö (SSE / [n - 2]) = Ö MSE (click me)

The variance of the error term should take on different values associated with different x values in a given regression analysis. True False (click one)

The variance of the error term is also known as _________.

3. Inference on the Slope, b ₁

(A) Performing a Test of Hypothesis on the Slope of the Regression Line-

(1) If the population slope b ₁ = 0, then x is not a good predictor of y.

(click me)

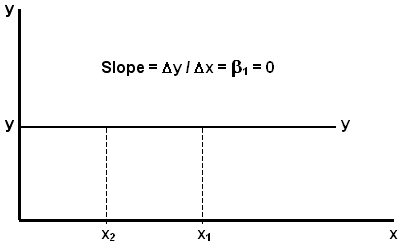
(2) If the population slope b ₁ > 0, then x and y have a positive relationship. (click me)

(3) If the population slope b ₁ < 0, then x and y have a negative relationship. (click me)

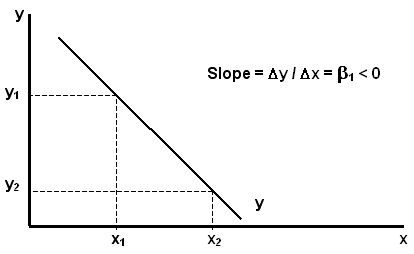
(B) Two tail tests

(1) Two-tail hypothesis:

H_o: b ₁= 0 ( equals zero)

H_a: b ₁¹ 0 ( does not equal zero)

(2) Table statistic for two-tail test: (critical value)

t _{a

/2,(n - 2 )} (click me)

(3) Computed statistic: (for all tests)

t* = [b₁ - b ₁] / S_b1

= [b₁ - b ₁] / [ s / Ö SS_x ]

where,

(a) S_b1 = Standard Error of the Coefficient = s / Ö SS_x_{(click me)}

(b) s = Ö s² = Ö (SSE / [n - 2]) = Ö MSE

(c) SSE = S (y - yhat)² = SS_y - [SCP_xy ]² / SS_x

(d) SS_y = S y²- (S y)² / n

(e) SCP_xy = S xy - (S x)(S y) / n

(f) SS_x = S x²- (S x)² / n

(4) Two Tail Hypothesis Test on the Slope of the Regression Line

H_o: b ₁= 0

H_a: b ₁_¹0

Reject H_o if |t*| > t _{a

/ 2,(n - 2)}

FTR(Support) H_o if |t*| £ t _{a / 2,(n - 2)}

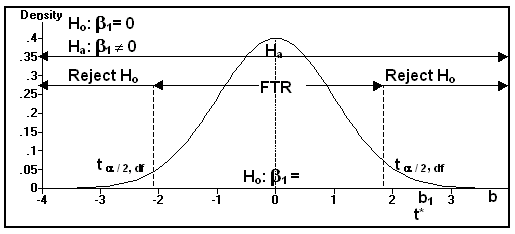
(5) The position of t* is determined by b_1.

(C) One tail test right:

(1) One-tail right hypothesis:

H_o: b ₁£ 0 ( equal to or less than zero)

H_a: b ₁> 0 ( greater than zero)

(2) Table statistic for one-tail test right: (critical value)

t _{a,

(n - 2 )}(full a and n - 2)

(3) Computed statistic: (for all tests)

t* = [b₁ - b ₁] / S_b1

(4) One Tail Hypothesis Test (Right) on the Slope of the Regression Line

H_o: b ₁_£0

H_a: b ₁> 0

Reject H_o if t* > t _{a,

(n - 2)}

FTR(Support) Ho if t* £ t _{a, (n - 2)}

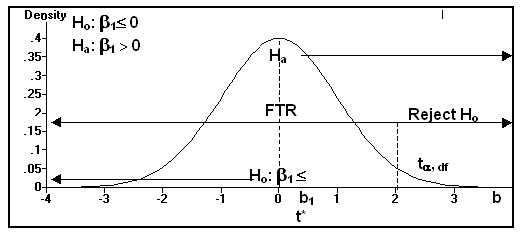
(5) The position of t* is determined by b₁.

(D) One tail test left:

(1) One-tail left hypothesis:

H_o: b₁³ 0 ( equal to or grater than zero)

H_a: b₁< 0 ( less than zero)

(2) Table statistic for one-tail test right: (critical value)

- t _{a,

(n - 2 )}(full a and n - 2)

(3) Computed statistic: (for all tests)

t* = [b₁ - b ₁] / S_b1

(4) One Tail Hypothesis Test (Left) on the Slope of the Regression Line

H_o: b ₁_³0

H_a: b ₁< 0

Reject H_o if t* < - t _{a,

(n - 2)}

FTR(Support) H_o if t* ³ - t _{a, (n - 2)}

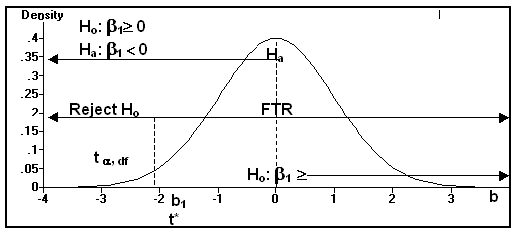
(5) The position of t* is determined by b₁.

(E) Confidence Interval for b ₁

(1) ± t _{a

/ 2,(n - 2)} = [b₁ - b ₁] / S_b1(solve for b ₁)

(2) CI for b ₁= b₁ ± [t _{a

/ 2,(n - 2)}]S_b1

(a) b₁ (sample statistic) is the point estimate of b ₁ (population parameter).

(b) t _{a

/ 2, (n - 2)} is the table t value which measures the number of standard errors of the coefficient.

(c) S_b1 is size of each standard error of the coefficient.

The confidence interval for b ₁ uses a different standard error of the coefficient than used an hpothesis test on b ₁. True False (click one)

Statistical evidence against H_o: b₁³ 0 is found in the ______ tail of the distribution.

4. Measuring the Strength of the Model: Coefficient of Determination

(A) Coefficient of Determination-

(1) Measures the percentage of variation in the dependent variable explained by the regression line.

(2) The variation of the observed value, y, from the average value, ybar.

(3) total variation

= explained variation + unexplained variation

= 100%

(4) SS_y = SSR + SSE

(a) SS_y = total variation (click me)

(b) SSR = explained variation (click me)

(c) SSE = unexplained variation (click me)

(5) SS_y/ SS_y = SSR /SS_y + SSE /SS_y

(a) 1 = SSR / SS_y + SSE / SS_y

(b) (SSR / SS_y)100 = % of variation of y explained by the position of the regression line.

(c) (SSE / SS_y)100 = % of variation of y unexplained by the position of the regression line.

(6) r² = 1 - SSE / SS_y = SSR / SS_y

(a) SS_y = S( y - ybar)² = S y² - (S y)² / n

(b) SSR = S(yhat - ybar)² = (SCP_xy)² / [SS_x]

(c) SSE = S(y - yhat )² = SS_y - [SCP_xy]²/SS_x

where,

[1] SCP_xy = S xy - (S x)(S y) / n

[2] SS_x = S x²- (S x)² / n

[3] SS_y = S y² - (S y)² / n

(7) Also note: If r = [SCP_xy] / (ÖSS_x)(ÖSS_y)

then: r² = { [SCP_xy] / (ÖSS_x)(ÖSS_y) }² = [SCP_xy]² / (SS_x)( SS_y)

If the regression line were flat with slope of zero, and Yhat = Ybar, which of the following would be equal to zero? SSy SSR SSE (click one)

If all the ordered pairs fall on the regression line, then _______ is equal to zero.

Once you have finished you should:

Go on to Regression Analysis: Examples
or
Go back to Regression Analysis: Activities and Assignments

Please reference "BA501 (your last name) Assignment name and number" in the subject line of either below.

E-mail Dr. James V. Pinto at BA501@mail.cba.nau.edu
or call (928) 523-7356. Use WebMail for attachments.