Correlation

BA501 : The Class : Stats : Correlation : Introduction
Correlation Analysis

§ Lesson 1- Introducton §

Correlation analysis results in a correlation coefficient, r, which measures the degree of linearity between the bivariate data, the ordered pairs x and y. The coefficient answers the question, "How well do the ordered pairs line up in a straight line?". If they all are in a straight line, the results either perfect positive linear relationship or a perfect negative linear relationship. If the ordered pairs are randomly and uniformly scattered, there is no linear relationship (shotgun effect). Correlation does not reflect a cause and effect relationship.

§ Bivariate Data § Coefficient of Correlation §

§ Correlation Conceptual Formula § Correlation Computing formula §

§ Two-Tailed Hypothesis Test § One tail (Left) Hypothesis Test §

§ One tail (Right) Hypothesis Test §

(1) Bivariate data- two variables, x and y.

(A) Ordered pairs, [ x, y ] are plotted in two dimension diagram.

(B) Ordered pairs must stay together (can not mix).

_{What is the minimum number of ordered pairs necessary to form a straight line?
One
Two
Three
(click one)}

(2) Coefficient of Correlation, r, measures the strength of the linear relationship within a sample of n bivariate data.

(A) How well do the ordered pairs line up in a straight line?

(B) r = 0 shotgun effect (click me)

(C) r = + 1 perfect positive correlation (click me)

(D) r = - 1 perfect negative correlation

(E) r = +0.8 strong positive correlation (click me)

(F) r = - 0.9 strong negative correlation

(G) r = 0.4 weak positive correlation

(H) r = - 0.35 weak negative correlation

(I) Slope can not be used to determine r. (click me)

(J) Properties of r:

[1] range: - 1 £ r £ + 1

[a] r = - 1 indicates a perfect negative linear relationship between x and y.

[b] r = + 1 indicates a perfect positive linear relationship between x and y.

[c] r does not have units of measure attached; but, slope does. (click me)

[2] The larger |r| , the stronger the linear relationship between x and y.

[3] r = 0 indicates no linear relationship between x and y.

[4] The signs of r and slope are always the same. (click me)

A perfect positive correlation between x an y indicates that x causes y to occur. True False (click one)

A shotgun effect in the ordered pairs indicates a correlation coefficient of ______.

(3) Correlation Conceptual formula: (do not use for hand calculations)

(A) r = S[x - xbar][y - ybar] / Ö [S (x - xbar)²]Ö [S (y - ybar)²]

The value of r depends on the relationship between x with xbar and y with ybar as seen in the following diagram.

(B) Diagram: (click me)

For a positive correlation, the majority of the ordered pairs would fall in the top right and bottom right panels. True False (click one)

(4) Correlation Computing formula: (use this one for hand calculations)

(A) r = [Sxy - (Sx)(Sy) / n] / Ö [Sx²- (Sx)² / n] Ö [Sy²- (Sy)² / n] (click me)

(B) = SCP_xy / Ö [SS_x ]Ö [SS_y ]

where,

[1] SCP_xy = [S ( x )( y ) - (Sx )(Sy ) / n]

(Sum of Cross Products x and y)

[2] SS_x = [Sx² - (Sx )² / n ]

(Sum of Squares x)

[3] SS_y = [Sy² - (Sy )² / n ]

(Sum of Squares y)

(C) SS_x and SS_y are numerators of variances.

[1] S_x² = [Sx² - (Sx)² / n] / [n - 1] = [SS_x ] / [ n - 1]

[2] S_y² = [Sy² - (Sy)² / n] / [n - 1] = [SS_y ] / [ n - 1]

If SSy and SSx are always positive, the sign of the correlation coefficient, r, must be determined by the sign of SCPxy. True False (click one)

Which Sum of Squares is equal to S(x - xbar)²?

(5) Two-Tailed Hypothesis test on Population Correlation Coefficient, r (rho = roe)

(click me)

H_o: r = 0

H_a: r ¹ 0

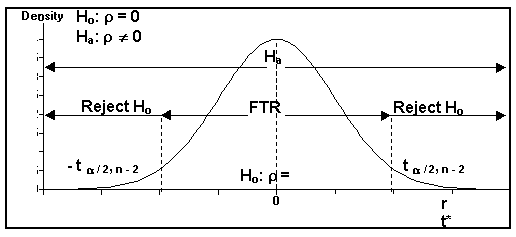
(A) Computed value: t* = r / Ö[(1 - r²) / (n - 2)]

(B) Table statistic: t a _{/2,(n - 2)}

(C) This example shows r and t* in the right tail; thus, reject Ho.

Two Tail Hypothesis Test on Correlation Coefficient, r

H_o: r = 0

H_a: r ¹ 0

Reject H_o if |t*| > t _a _{/ 2,(n - 2)}

FTR(Support) H_o if |t*| £ t _a _{/ 2,(n
- 2)}

You must have a standard error of the correlation coefficent in order to calculate t*. True False (click one)

Supporting Ho in a two-tail hypothesis test is a strong conclusion i.e Rho is equal to zero. Rejecting Ho in the same test leads to a ______ conclusion.

(6) One tail (Left) Hypothesis test on Population Correlation Coefficient on r

(click me)
(A) One-tail left hypothesis:

H_o: r ³ 0

H_a: r < 0

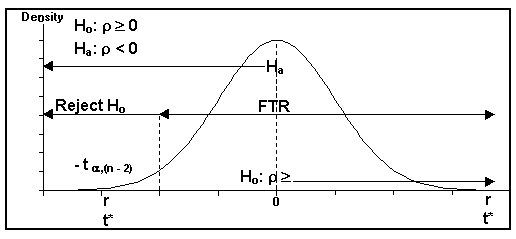
(B) Table statistic: t _a _{,(n - 2)}

(C) Computed value: t* = r / Ö[(1 - r²) / (n - 2)]

(D) This example shows r and t* in the left tail; thus, reject Ho.

One Tail Hypothesis Test (Left) on Population Correlation Coefficient, r

H_o: r _³0

H_a: r < 0

Reject H_o if t* < - t _a _{,(n - 2)}

FTR(Support) H_o if t* ³ - t _a _{,(n
- 2)}

Which end of the distribution would r be located to show extreme statistical evidence against H_o: r ³ 0 ? Left Right (click one)

(7) One tail (Right) Hypothesis Test on Population Correlation Coefficient, r

(click me)

(A) One-tail right hypothesis:

H_o: r £ 0

H_a: r > 0

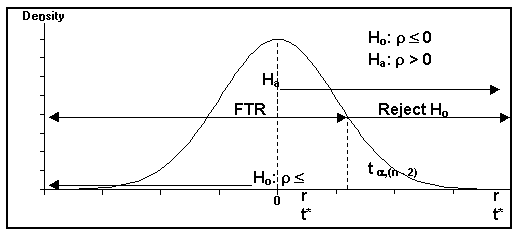
(B) Table statistic: t _{a,(n
- 2)}

(C) Computed value: t* = r / Ö[(1 - r²) / (n - 2)]

(D) This example shows r and t* not in the tail; thus, FTR(Support) Ho.

One Tail Hypothesis Test (Right) on Population Correlation Coefficient, r

H_o: r £ 0

H_a: r > 0

Reject H_o if t* > t _a _{, (n - 2)}

FTR(Support) H_o if t* £ t _a _{, (n
- 2)}

For H_o: r £ 0 can r be greater than zero and still support this hypothesis? Yes No (click one)

Extreme statistical evidence against H_o: r £ 0 is found on the ______ tail of the distribution.

Once you have finished you should:

Go on to Lesson 2: Examples
or
Go back to Correlation Analysis: Activities and Assignments

Please reference "BA501 (your last name) Assignment name and number" in the subject line of either below.

E-mail Dr. James V. Pinto at BA501@mail.cba.nau.edu
or call (928) 523-7356. Use WebMail for attachments.