





 |
 |
 |
 |
  |
|
§ Excel and Equations §
Excel- commands used in this topic (Excel in Office 97 and Office 2000)
§ Confidence Intervals using Z §
§ Confidence Intervals using t §
§ Probability of xbar values (left tail) §
§ Probability of xbar values (right tail) §
§ xbar value associated with a given probability (left tail) §
§ xbar value associated with a given probability (right tail) §
§ table Z § table t § Equations §
1. Confidence Intervals using Z
Click on Paste Function-Statistical-Confidence. This results in the maximum error (E). Add E to xbar to get the upper limit of the confidence interval. Subtract E from xbar to get the lower limit of the confidence interval. If the sample size is large, you can also use the next procedure.
2. Confidence Intervals using t
Click on Tools-Data Analysis-Descriptive Statistics. Check the Confidence Level for the Mean box and put in the confidence level you desire in the box to the right. This results in the maximum error (E). Add E to xbar to get the upper limit of the confidence interval. Subtract E from xbar to get the lower limit of the confidence interval. If Data Analysis does not show up, then click on Tools-Addins and select the top two options of Analysis Pack and Analysis Pack VBA.
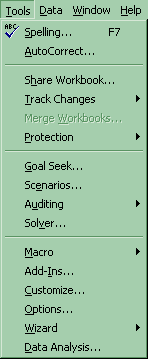
Finding the confidence interval using individual steps:
Finding the confidence interval using Tools-Data Analysis-Descriptive Statistics-Summary Statistics-Confidence Level for Mean:
3. Probability of xbar values (left tail)
For the probability (left tail) of a range of xbar values in the Normal distribution: Paste Function-Statistical-Normdist (cumulative = true yields the cumulative probability; cumulative = false yields the probability mass function.) Put xbar in the x box. Put the standard error of the mean in the standard deviation box.
4. Probability of xbar values (right tail)
For the probability (right tail) of a range of xbar values in the Normal distribution: Paste Function-Statistical-Normdist (cumulative = true yields the cumulative probability; cumulative = false yields the probability mass function.). Put the standard error of the mean in the standard deviation box. Then in another cell put =1 - (cell reference to Normdist). Put xbar in the x box. See Probability of xbar values (left tail) above.
5. Xbar value associated with a given probability (left tail)
For an xbar value associated with a given probability (left tail) in the Normal distribution: Paste Function-Statistical-Norminv. Put the standard error of the mean in the standard deviation box.
6. Xbar value associated with a given probability (right tail)
For an xbar value associated with a given probability (right tail) in the Normal distribution: Paste Function-Statistical-Normdinv. Put the standard error of the mean in the standard deviation box. Then in another cell put =1 - (cell reference to Norminv). See Xbar value associated with a given probability (left tail) above. Assuming that the probability is in cell A1, mean in B1, SEMean in C1, this is what the cell formula should look like:
7. Table Z values
Place a confidence level (e.g. 90, 95, 99 etc.) into any cell, say A1. Click on Paste Function-Statistical-Normsinv. Reference the confidence level cell for Probability. Modify the resulting cell formula as follows: =NORMSINV(A1/100/2+0.5)
Assuming that the probability is in cell A1, then formula should be modified as follows:
8. Table t values
Place a confidence level (e.g. 90, 95, 99 etc.) into any cell, say A1. Place the degrees of freedom (n -1) into any cell, say B5. Click on Paste Function-Statistical-tinv. Reference the confidence level cell for Probability. Reference the degrees of freedom cell. Modify the resulting cell formula as follows: =TINV(1-A1/100,B5)
Assuming the confidence level is in A1 and the degrees of freedom in B5, your modified cell formula should look like this:
Sampling Distributions and Confidence Intervals
Equations
§ CLT without replacement finite population §
§ Z or t? § Z score and t scores §
§ Confidence Intervals § CI Interpretations §
§ Sample Size §
1. Central Limit Theorem
Central Limit Theorem (CLT): for infinite population and sampling with replacement from a finite population.
(a) mxbar = m
(b) sxbar = s /Ön
2. CLT without replacement finite population
Central Limit Theorem (CLT): using finite population correction factor (fpc): for sampling without replacement from a finite population.
If n / N < 0.05 do not use fpc, or,
n / N ³ 0.05 must use fpc
(a) mxbar = m
(b) sxbar = [s /Ön][Ö(fpc)]
= [s /Ön][Ö( N - n )/( N - 1 )]
3. Z or t?
Source of Standard Deviation
| Population s | Sample s | ||
| Sample Size | Small df £ 30 |
Z |
t |
| Large df > 30 |
Z |
Z or t |
4. Z score and t scores
Zo = [xbaro - m] / [s /Ön] or
to = [xbaro - m] / [ s /Ön]
5. Confidence Intervals
(1 - a)% CI for m = xbar ± [Za/2][s/Ön] or
(1 - a)% CI for m = xbar ± [t a/2,df ][ s / Ön]
6. CI Interpretations
Three Interpretations of CI:
(a) I am (1 - a )% confident that the population m lies between lower limit value and upper limit value of the CI.
(b) If I repeatedly obtained samples of same size, then (1 - a )% of the resulting CI's would capture m and a% would not.
(c) I am (1 - a)% confident that my estimate of m (point estimate xbar) is within one Maximum Error (E) of the actual value of m.
7. Sample Size
E = [Z a/2][s /Ön]
n = {[Za/2] [s] / E}²
s » [H - L] / 4
Go on to Home
Work
or
Go back to Sampling
Distributions and Confidence Intervals
Please reference "BA501 (your last name) Assignment name and number" in the subject line of either below.
E-mail Dr. James V. Pinto at
BA501@mail.cba.nau.edu
or call (928) 523-7356. Use WebMail for attachments.

Copyright 2002 Northern
Arizona University
ALL RIGHTS RESERVED