BA501 : The Class : Stats : Measures : Excel
Descriptive Measures: Excel and Equations

---

§ Excel and Equations §

§ Mode § Range § Sample Variance §

§ Population Variance § Sample Standard Deviation §

§ Population Standard Deviation § Z Score §

§ Equations §

---

Excel Steps-

Sample Mean

(1) Use the paste function on the tool bar. Click Paste Function-Statistical-Average.

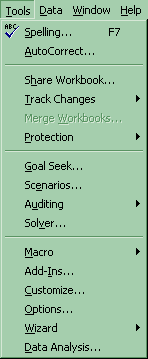
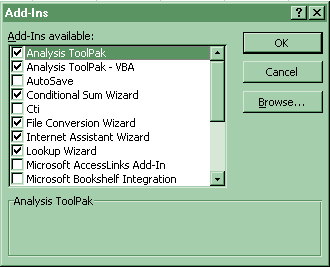
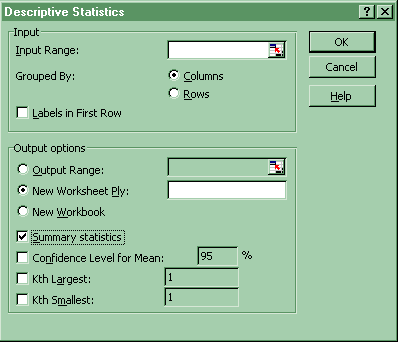
(2) Click on Tools-Data Analysis-Descriptive Statistics-Summary Statistics . If Data Analysis does not show up, then click on Tools-Addins and select the top two options of Analysis Pack and Analysis Pack VBA.

Population Mean

Use the paste function on the tool bar. Click Paste Function-Statistical-Average. (See Sample Mean above)

Median

(1) Use the paste function on the tool bar. Click Paste Function-Statistical-Median.

 

(2) Click on Tools-Data Analysis-Descriptive Statistics-Summary Statistics . If Data Analysis does not show up, then click on Tools-Addins and select the top two options of Analysis Pack and Analysis Pack VBA. (See Sample Mean (2) above)

Mode

(1) Use the paste function on the tool bar. Click Paste Function-Statistical-Mode.

(2) Click on Tools-Data Analysis-Descriptive Statistics-Summary Statistics . If Data Analysis does not show up, then click on Tools-Addins and select the top two options of Analysis Pack and Analysis Pack VBA. (See Sample Mean (2) above)

Range

Click on Tools-Data Analysis-Descriptive Statistics-Summary Statistics . If Data Analysis does not show up, then click on Tools-Addins and select the top two options of Analysis Pack and Analysis Pack VBA. (See Sample Mean (2) above)

Descriptive Measures

Equations

§ Sum of Deviations § Sample Mean § Population Mean §

§ Median § Range § Sum of the Squared Deviations §

§ Variance § Standard Deviation § Empirical Rule §

§ Z Score § Other Equations not found at this topic site §

Equations found at this topic site:

1.  Sum of Deviations

Sd = S(x - xbar) = 0

d = individual deviation

x = data value

xbar = sample mean =

2. Sample Mean

xbar = Sx / n =

S means sum

x = data value

n = number of data values in sample

3.  Population Mean

m = Sx / N

S means sum

x = data value

N = number of data values in the population

4.  Median

= Md

(a) When n is odd,

Md = (n + 1) / 2 position in order array (find data value in that position)

(b) When n is even,

Md = (two middle values) / 2

5. Range

= high data value - low value

R = H - L

6.  Sum of the Squared Deviations

Sd² = S(x - xbar)²

d² = (individual deviation) ²

x = data value

xbar = sample mean =

7. Variance

(a) Conceptual Formulae:

(1) Conceptual Formula Sample Variance

s² = Sd² / (n - 1) = S(x - xbar)² / (n - 1)

(not for hand calculations)

S means sum

d² = (individual deviation)² = (x - xbar)²

n = number of data values in sample

xbar = Sx / n = sample mean =

x = data value

(n - 1) = degrees of freedom

(2) Conceptual Formula Population Variance

s² = S(x - m)² / N

S means sum

x = data value

m = Sx / N = population mean

N = number of data values in population

(b) Computing Formula Sample Variance

s² = [Sx² - (Sx)² / n] / (n - 1) (use for hand calculations)

x = data value

n = number of data values in sample

8. Standard Deviation

(a) Conceptual Formula Sample Standard Deviation

Sample s = Ö[s²] = Ö[Sd² / (n - 1)]

= Ö[S(x - xbar)² / (n - 1)]

(not for hand calculations)

Ö = square root

S means sum

d² = (individual deviation)² = (x - xbar)²

n = number of data values in sample

xbar = Sx / n = sample mean =

x = data value

(n - 1) = degrees of freedom

(b) Computing Formula Sample Standard Deviation

s = Ös² = Ö{[Sx² - (Sx)² / n] / (n - 1)}

(use for hand calculations)

x = data value

n = number of data values in sample

9. Empirical Rule

(a) 68% of data values between xbar ± s

(b) 95% of data values between xbar ± 2s

(c) 99.7% of data values between xbar ± 3s

 10. Z Score

Z = [x - xbar] / s

x = data value

xbar = mean (sample) =

[x - xbar] = individual deviation

s = standard deviation (the average deviation)

Other Equations not found at this topic site:

§ Midrange § Mean Absolute Deviation §

§ Coefficient of Variation §

§  Percentile § Interquartile Range §

§ Pearsonian Coefficient of Skewness §

§ Chebyshev's Inequality §

§ Grouped Data § Coding Data §

1. Midrange

Mr = the average of the lowest (L)

and highest (H) data values.

Mr = [(L) + (H)] / 2

2. Mean Absolute Deviation

MAD = (S|x - xbar|) / n

S means sum

x = data value

xbar = Sx / n = sample mean =

n = number of data values in sample

3. Coefficient of Variation

CV = [s / xbar]100

s = sample standard deviation

xbar = sample mean =

4. Percentile

P(%) = [ n ][% / 100 ]

% = the percentile

n = number of data

P(%) = position in ordered array

5. Interquartile range

IQR = 3rd Quartile - 1st Quartile

6. Pearsonian coefficient of skewness-

Sk = 3[xbar - Md] / s

xbar = sample mean =

Md = median

s = sample standard deviation

7. Chebyshev's Inequality-

(a) At least 75% of data values between xbar ± 2s

(b) At least 89% of data values between xbar ± 3s

xbar = sample mean =

s = sample standard deviation

8. Approximating statistics from grouped data

(a) Sample Mean, xbar =

xbar » [Sf(m)] / n,

f is the class frequency

m is the class midpoint

n is the sample size

(b) Sample Standard Deviation, s

s » Ö{ [Sf(m)² - (Sfm)² / n] / [n - 1] },

f is the class frequency

m is the class midpoint

n is the sample size

10. Coding Data Values

(a) Rules for Subtraction and Addition of C:

(1) If C subtracted from original data:

actual xbar = xbar_adj + C

S_adj = actual S

(2) If C added from original data:

actual xbar = xbar_adj - C

S_adj = actual S

(b) Rules for Multiplication and Division by C:

(1) If C divided into original data:

actual xbar = [xbar_adj ] [ C ]

actual S = [S_adj ] [C]

(2) If original data multiplied by C:

actual xbar = [xbar_adj ] / [ C ]

actual S = [S_adj ] / [C]