Introduction
In this exercise, we will examine exploiting locality/cache reuse by tiling main memory accesses.
Problem Description
The CPU uses a multi-level cache to reduce the number of (slow) accesses to main memory. When data is accessed in memory, it is stored in this cache. Therefore, if the program accesses the same memory locations within a short time interval, data may still reside in cache, and accessing main memory can be avoided.
Examining Figure 3, the row-wise memory access pattern (comparing each point to all other points in the dataset before computing the next row), has poor cache reuse. Observe that for large N, after the row corresponding to p0 has computed the data points at the start of the dataset (e.g., p0, p1, p2, p3, …) will have been flushed from cache by the time the row corresponding to p1 is to be computed.

Figure 3: Illustrative example of the order of calculations carried out when computing the distance matrix. Each row/point is compared to all other columns before computing the next row.
A clever trick to improve cache reuse is to tile the computation. Instead of iterating over each row, the data is accessed in 2-D tiles. Therefore, when computing the distances between points, there is a greater chance that data resides in cache and will not need to be accessed in main memory.
Figure 4 shows an example where there are N=12 points. The data is no longer accessed in a row-wise fashion. Rather tiles of 3×3 points are accessed consecutively.
-
From Figure 3, when computing each row at a time, dist(p0,p0) (on row p0) and dist(p1,p0) (on row p1) were N data point pair accesses apart.
-
In contrast, using the 3×3 tile, dist(p0,p0) (on row p0) and dist(p1,p0) (on row p1) are only 3 data point pair accesses apart (Figure 4). Thus, there is a greater chance that relevant data will reside in cache.
Figure 4: Illustrative example where N=12. The distances between points are computed using tiles of size 3×3 (b=3). The numbers represent the tiles and the order in which the distance matrix will be computed.
Programming Activity 2
Make a copy of the row-wise distance matrix program. Implement the tiling algorithm described above, where the points assigned to each process rank remains the same. When executing your experiments, use the same guidelines as in Programming Assignment #1 (e.g., compile with -O3, use a single node, use the exclusive flag, etc.).
In your solution, you must perform the following tasks:
- You will experimentally determine a good value for b (values given below).
- We will use a square b×b tile. However, note that b may not evenly divide N/p (rows) or N (columns). Thus, when the b×b tile does not evenly divide the rows and columns, dynamically reduce the tile size as appropriate. For example, if N=8, then when computing across rows, you will need to reduce the size of tile 2 (see Figure 5).
- Only use p=20 process ranks.
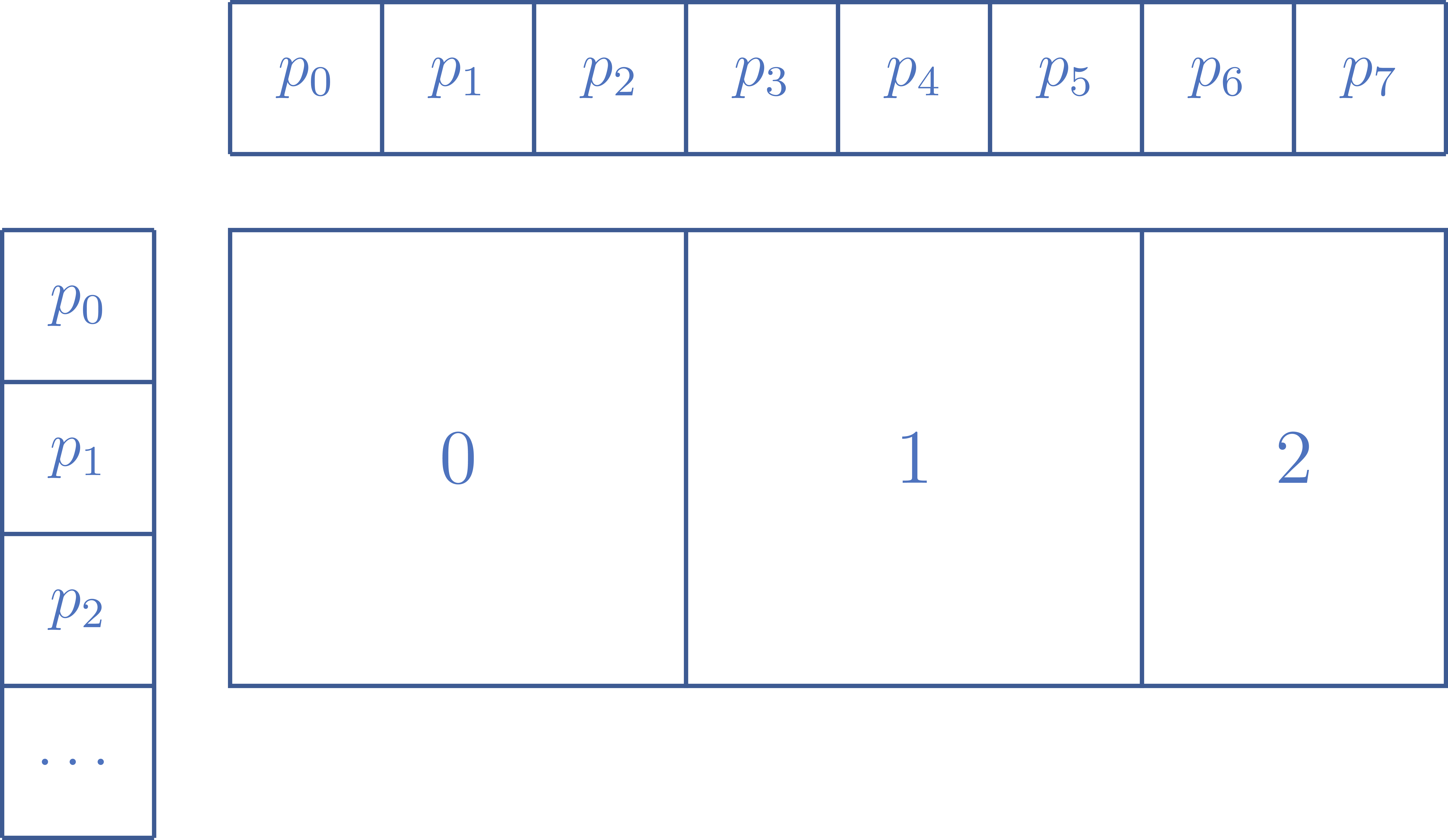
Figure 5: Illustrative example where N=8 and b=3. The tile size does not divide evenly into the number of rows and columns. Tiles 0 and 1 compute 9 point pairs, tile 2 computes 6 point pairs.
In your report, include a Table with the following information. The report must include the tile size b for the values given below, the response time (s), the global sum used for validation, and the job script name that you used to obtain these results. The job script may be the same for all executions. Include all job scripts in the submitted archive. A template table is provided below.
| b | Time (s) | Global Sum | Job Script Name (*.sh) |
|---|---|---|---|
| 5 | |||
| 100 | |||
| 500 | |||
| 1000 | |||
| 2000 | |||
| 3000 | |||
| 4000 | |||
| 5000 |
Using the value of b that yielded the best performance (lowest response time), compute the same table as the row-wise distance calculation. A template table is provided below.
| # of Ranks (p) | Time (s) | Parallel Speedup | Parallel Efficiency | Global Sum | Job Script Name (*.sh) |
|---|---|---|---|---|---|
| 1 | |||||
| 4 | |||||
| 8 | |||||
| 12 | |||||
| 16 | |||||
| 20 |
Answer the following questions:
- Q7: When tiling the computation, comparing all values of b, does b=5 or b=5000 achieve the best performance? Why do you think that is?
- Q8: Does tiling the computation improve performance over the original row-wise computation? For p=20 process ranks, report the speedup of the tiled solution using the best value of b over the row-wise solution.