|
|||||
|
|
|
|
|
|
§ Continuous Probability §
Lesson 2- Examples
§ 1. P[0 £ Z £ z1] § 2. P[- z1 £ Z £ 0] §
§ 3. P[- z1 £ Z £ z2] § 4. P[Z £ z1] §
§ 5. P[Z ³ - z1] § 6. P[Z ³ z1] § 7. P[Z £ - z1] §
§ 8. P[z1 £ Z £ z2] § 9. P[- z1 £ Z £ - z2] §
§ Examples 10 - 13 §
Example 1
P[0 £ Z £ z1] = P[ 0 £ Z £ 1.5 ] = 0.4332 See figure below. Look up 1.5 in the Z table to get the answer.
(click me). Use Excel to solve this problem.
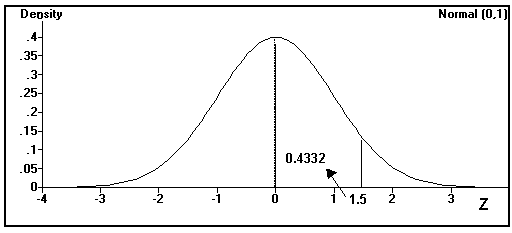
What probability does Excel give associated with Z =< 1.5? 0.9332
0.0668
(click one)
Example 2
P[- z1 £ Z £ 0] = P[ - 1.5 £ Z £ 0 ] = 0.4332 You can look up the positive version of Z = 1.5 in the Z table to get the answer since negative Zs are not in this table.
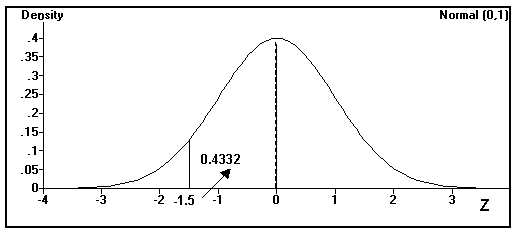
What probability does Excel give associated with Z =< - 1.5? 0.9332
0.0668
(click one)
Example 3
P[- z1 £ Z £ z2] = P[ - 1.5 £ Z £ 1.5 ] = 0.4332 + 0.4332 = 0.8664 You can look up Z = 1.5 in the Z table and multiply it by 2 to get the answer.
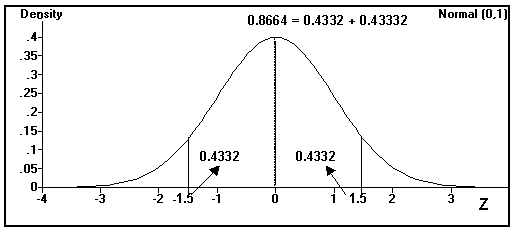
In Excel one must subtract the probability associated with Z =< -1.5 from
the probability associated with Z =< 1.5 to get the answer of 0.8664. True
False
(click one)
Example 4
P[Z £ z1] = P[Z £ 1.5 ] = 0.5 + 0.4332 = 0.9332 You can look up Z = 1.5 in the Z table and add the left side of the distribution (0.5000) to get the answer.
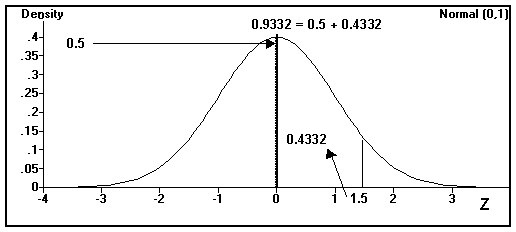
In Excel the answer to the last example is obtained in one step. True
False
(click one)
Example 5
P[Z ³ - z1] = P[Z ³ - 1.5 ] = 0.5 + 0.4332 = 0.9332 You can look up Z = 1.5 in the Z table and add the right side of the distribution (0.5000) to get the answer.
In Excel the answer to the last example is obtain in one step. True
False
(click one)
Example 6
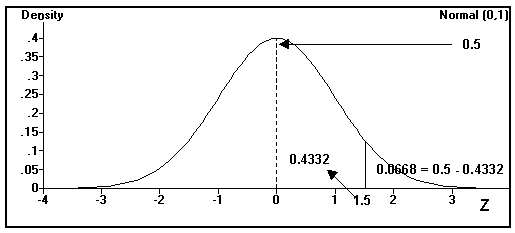
P[Z ³ z1] = P[Z ³ 1.5 ] = 0.5 - 0.4332 = 0.0668 You can look up Z = 1.5 in the Z table and subtract that probability from the right side of the distribution (0.5) to get the answer.
In Excel the answer to the last example is obtain in one step. True
False
(click one)
Example 7
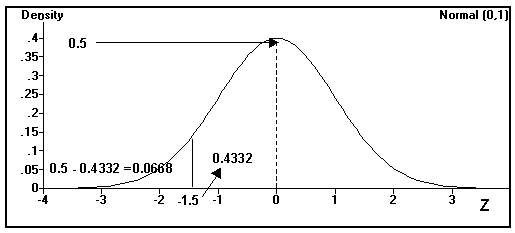
P[Z £ - z1] = P[Z £ - 1.5 ] = 0.5 - 0.4332 = 0.0668 You can look up the positive version Z = 1.5 in the Z table and subtract that probability from the left side of the distribution (0.5) to get the answer.
In Excel the answer to the last example is obtain in one step. True
False
(click one)
Example 8
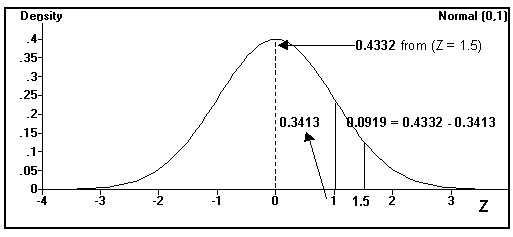
P[z1 £ Z £ z2] = P[ 1.0 £ Z £ 1.5 ] = 0.4332 - 0.3413 = 0.0919 You can look up Z = 1.5 in the Z table and subtract from that probability the probability associated with Z = 1.0 to get the answer.
In Excel one must subtract the probability associated with Z =< 1.0 from
the probability associated with Z =< 1.5 to get the answer of 0.0919. True
False
(click one)
Example 9
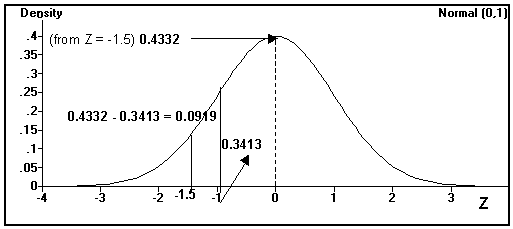
P[- z1 £ Z £ - z2] = P[ -.1.5 £ Z £ - 1.0 ] = 0.4332 - 0.3413 = 0.0919 You can look up Z = 1.5 in the Z table and subtract that probability from the probability associated with Z = 1.0 to get the answer. Use Excel to solve this problem.
In Excel one must subtract the probability associated with Z =< -1.5 from
the probability associated with Z =< -1.0 to get the answer of 0.0919. True
False
(click one)
Examples 10 - 13
§ 10. P[Z £ z1] = 0.90 § 11. P[Z £ - z1] = 0.15 §
§ 12. (a) P[x > 300] (b) P[225 £ X £ 300] §
§ 13. P[X £ xo] = 0.75 §
Download Examples
10 - 13 to save to disk. (optional)
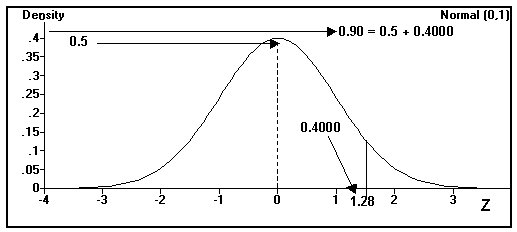
Example 10
Find the value of z for the following probability statement.
P[Z £ z1] = 0.90
= 0.50 + 0.40
Look up 0.4000 in the body of the Z table to find the associated Z score.
z1 = 1.28
Use Excel to solve this problem.
In Excel which command is used to give a Z score given that you have a known probability?
Normsdist
Normsinv
(click
one)
Example 11
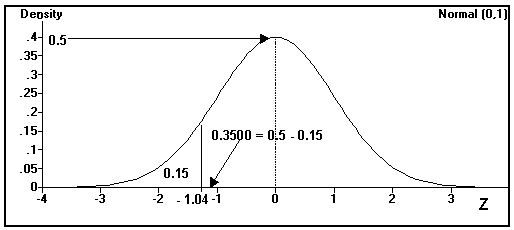
Find the value of z for the following probability statement.
P[Z £ - z1] = 0.15
= 0.50 - 0.35
Look up 0.3500 in the body of the Z table to find the associated Z score.
z1 = - 1.04
Use Excel to solve this problem.
In Excel one would look up 0.3500 using the Normsinv command to obtain the Z
score, Z = - 1.04. True
False
(click
one)
Example 12 (a)
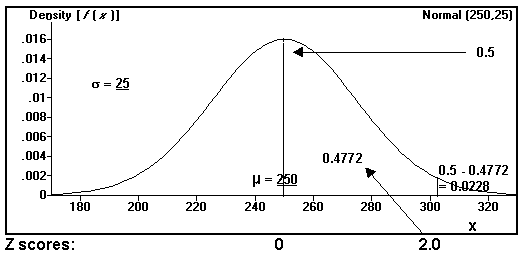
Assume a normally distributed population of the life time of batteries with mean life time 250 minutes and standard deviation 25 minutes when used in an ordinary toy.
(a) What is the probability that a battery has a life time greater than 300 minutes when used in an ordinary toy?
m = 250
s = 25
P[x > 300] = P(Z ³ [x - m] / s )
= P(Z ³ [ 300 - 250] / 25)
= P(Z ³ 50 / 25 )
= P(Z ³ 2.0 )
= 0.5 - 0.4772
= 0.0228
Use Excel to solve this problem.
In Excel which command is used to give a probabilty given that you have a known
Z score? Normsdist
Normsinv
(click
one)
Example 12 (b)
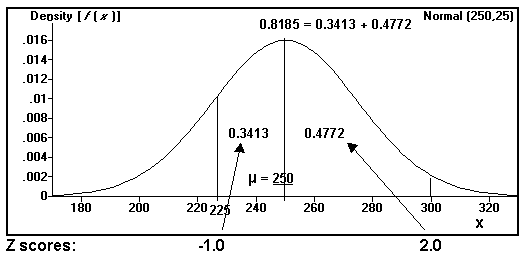
What is the probability that a battery has a life time between 225 and 300 minutes when used in an ordinary toy?
m = 250
s = 25
P[225 £ X £ 300] = P([ x1 - m]s / £ Z £ [x2 - m ] / s )
= P( 225 - 250 ] / 25 £ Z £ [ 300 - 250] / 25)
= P(- 25 / 25 £ Z £ 50 / 25)
= P( - 1.0 £ Z £ 2.0 )
= 0.3413 + 0.4772
= 0.8185
Use Excel to solve this problem.
In Excel one would substract the probability associated with Z = -1.0 from the
probability associated with Z = 2.0 to obtain the answer 0.8185. True
False
(click
one)
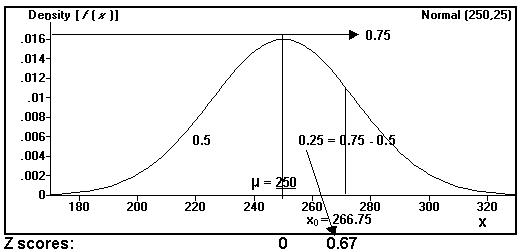
Example 13
Assume a normally distributed population of the life time of batteries with mean lifetime 250 minutes and standard deviation 25 minutes when used in an ordinary toy. After what number minutes will 75% of the of the batteries be dead when used in an ordinary toy?
m = 250
s = 25
P[X £ xo] = 0.75
0.75 - 0.5 = 0.2500
Look up 0.2500 in the body of the Z table to find the associated Z score.
zo = 0.67
zo = [xo - m] / s
0.67 = [xo - 250] / 25
xo = 250 + [25][ 0.67 ] = 250 + 16.75 = 266.75
Use Excel to solve this problem.
In Excel which
command is used to give an "x" value given that you have a known probability?
Normdist
Norminv
(click
one)